Modélisation bayésienne du mix média avec des données limitées data

Si vous avez déjà rencontré des problèmes de modélisation du mix média (MMM) dans le domaine du marketing, vous savez peut-être qu'ils impliquent tout un ensemble d'effets spécifiques au canal (retards, saturation et effets à long terme) qui sont chacun modélisés par au moins un paramètre différent. Vous savez peut-être aussi qu'il ne s'agit pas exactement d'un contexte où l'abondance de data et/ou de data variabilité pour former votre modèle est garantie. Dans les MMM classiques, des hypothèses préalables sur le comportement des canaux médiatiques (c'est-à-dire sur les valeurs des paramètres susmentionnés) sont nécessaires pour évaluer la contribution de chaque canal aux ventes par le biais d'une régression linéaire. L'approche MMM bayésienne [1] constitue une alternative puissante à cette méthode, car elle permet une estimation globale du comportement des canaux et de l'augmentation des ventes par le biais de distributions préalables et de data. Cela permet d'éviter les hypothèses incorrectes et immuables si des études antérieures spécifiques au canal n'ont pas été réalisées. Inutile de dire que cela rend également le modèle beaucoup plus complexe et qu'il devient crucial de saisir toutes sortes d'informations susceptibles d'aider à trouver une bonne solution.

En effet, il y a un danger inhérent à laisser un modèle aussi complexe s'appuyer uniquement sur data pour apprendre : contrairement à la majorité des applications de problèmes de régression, un modèle MMM doit être un outil descriptif plutôt que prédictif. Ainsi, une bonne adaptation à data et une généralisation à data sont intéressantes mais ne suffisent pas : le modèle doit également fournir des informations correctes sur l'augmentation historique des ventes, le retour sur investissement(ROI) et la saturation pour chaque canal, afin de garantir un résultat fiable pour la planification des stratégies de marketing. En d'autres termes, le danger réside dans l'existence de plusieurs combinaisons de paramètres qui correspondent correctement au site data, étant donné qu'elles n'ont pas toutes un sens réel - on pourrait dire qu'il s'agit simplement d'une autre manifestation de la malédiction de la dimensionnalité.

Mais qu'est-ce que cela signifie pour une solution d'avoir un "sens réel" ? Une réponse viable est que, même si le modèle doit être libre d'apprendre de nouveaux modèles à partir de data, ses résultats ne doivent pas s'écarter complètement des connaissances commerciales antérieures qui pourraient être disponibles. En effet, la possibilité d'inclure ces informations en tant que connaissances préalables (afin d'aider le modèle à trouver une combinaison de paramètres judicieuse) n'est que l'un des aspects polyvalents et puissants de la solution bayésienne.

Dans cet article, nous verrons comment les connaissances qualitatives et quantitatives des entreprises peuvent être traduites en distributions préalables adaptées qui permettront d'obtenir un MMM performant, même lorsque les informations provenant de l'historique structuré data sont rares.

Avant d'explorer la manière dont nous pouvons exploiter les distributions de probabilités pour optimiser les performances de notre modèle, commençons par quelques définitions clés de la modélisation du mix média elle-même. Par essence, le MMM est basé sur une régression linéaire, où la variable dépendante est le chiffre d'affaires visé et les variables indépendantes (caractéristiques) sont l' investissement dans différentes actions de marketing, ainsi que des variables de contrôle externes qui ont également un impact sur les ventes (prix, concurrence, saisonnalité, etc.).

Il existe néanmoins une différence cruciale entre cette formulation et celle d'un modèle de régression linéaire conventionnel : Les caractéristiques de l'investissement marketing doivent également passer par un ensemble de transformations non linéaires, dont l'objectif principal est de représenter les comportements attendus des canaux médiatiques qui ne peuvent pas être modélisés par des correspondances linéaires. Ces transformations comportent chacune un sous-ensemble de paramètres qui contrôlent l'intensité et la nature globales de ces comportements. Il existe deux principaux mappages non linéaires, la saturation et le délai, qui seront brièvement abordés dans ce qui suit.

La saturation est un effet très connu des canaux de commercialisation, qui se traduit par une relation non linéaire entre l'investissement et les recettes qu'il engendre. Il peut s'agir de l'effet des publicités diffusées auprès d'utilisateurs de moins en moins pertinents, ou de l'augmentation relativement faible de la portée (nouveaux utilisateurs exposés) pour chaque dollar supplémentaire investi. L'effet de saturation peut être modélisé par l'équation de Hill décrite ci-dessous. L'expression exacte n'étant pas d'un grand intérêt ici, le lecteur est invité à se concentrer sur les figures 1a et 1b, qui montrent ce qu'il advient de la fonction de Hill lorsque les valeurs de ses deux paramètres sont modifiées.

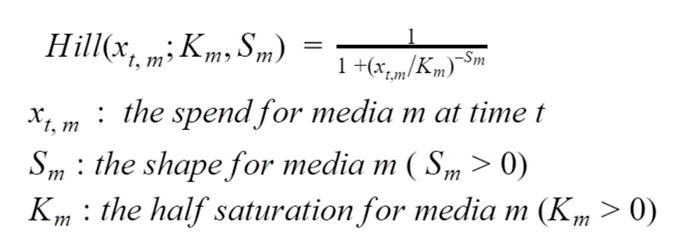
Equation 1. L'équation de Hill

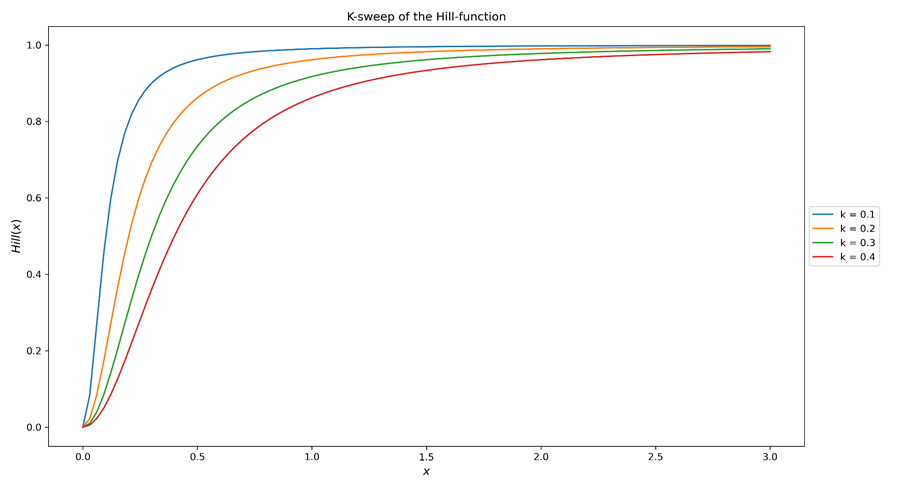
Figure 1a. Balayage du paramètre K (demi-saturation) de la fonction de Hill. La forme générale de la courbe est à peu près conservée tandis que le point de demi-saturation (où Hill(x)=0,5) est déplacé. En d'autres termes, plus K est grand, plus il est difficile de saturer le canal médiatique associé.

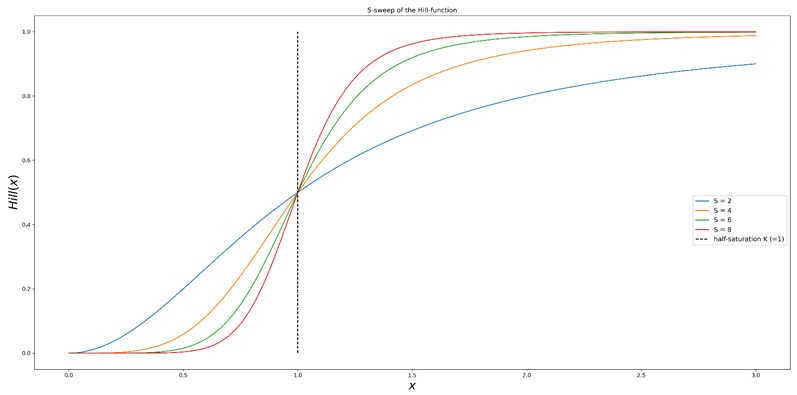
Figure 1b. Balayage du paramètre S (forme) de la fonction de Hill. Le point de demi-saturation de la courbe est conservé tandis que la pente autour de ce point augmente. En d'autres termes, plus S est grand, plus les gains marginaux des investissements autour du point de demi-saturation sont importants.

Comme indiqué ci-dessus, l'équation de Hill comporte deux paramètres importants : alors que K définit le point de demi-saturation (la chaîne se trouve exactement à la moitié de son revenu maximal lorsque l'investissement est égal à K), S interfère avec la forme de la courbe de saturation (plus sa valeur est élevée, plus la courbe prend la forme d'un S). Il est essentiel d'apprendre à estimer précisément K et S, car le niveau d'investissement optimal peut être extrait analytiquement à partir de ces paramètres. En effet, lorsqu'aucun autre effet n'est pris en compte, l'investissement qui produit un retour sur investissement (ROI) maximal peut être calculé comme suit :

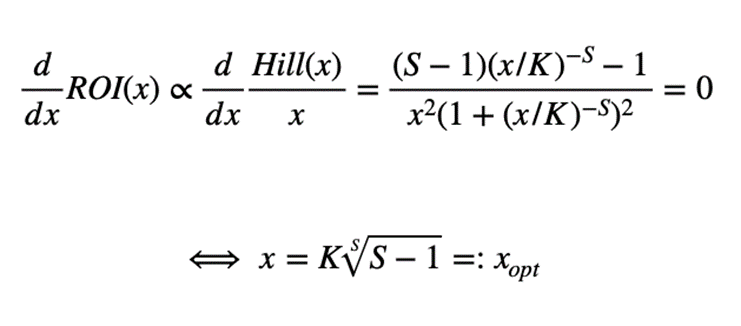
Équation 2. Dérivation du niveau d'investissement optimal à partir des paramètres de saturation

Notez que cet investissement optimal existe pour S>1 et qu'il est toujours compris entre une et trois fois la valeur de demi-saturation K (vous pouvez vous en assurer en vérifiant les valeurs que peut prendre la racine S).

Le deuxième effet à prendre en considération est l'allocation temporelle des recettes, après l'exécution d'un investissement spécifique au canal. En effet, les investissements et les recettes ne se produisent pas simultanément, et il peut s'écouler quelques semaines avant que les recettes ne deviennent significatives. En outre, certaines chaînes de médias sont vouées à avoir des effets plus localisés, tandis que d'autres chaînes peuvent conserver leurs investissements pendant de plus longues périodes, générant ainsi des recettes même après des périodes relativement longues. Ces deux aspects peuvent être modélisés par l'équation d'Adstock présentée ci-dessous, par les paramètres thêta et alpha respectivement. Le paramètre L ne doit pas être spécifique à chaque canal et ne peut être fixé qu'à une valeur fixe dont on sait empiriquement qu'elle est suffisamment grande, telle que L=13 (comme suggéré dans [1]). Une fois de plus, le lecteur est invité à se concentrer sur les figures 2a et 2b plutôt que sur l'équation 3.

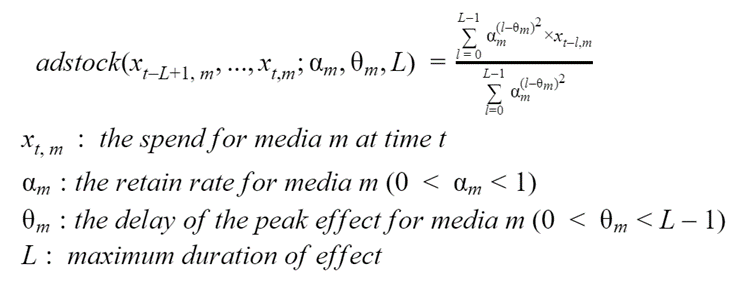
Équation 3. L'équation d'Adstock

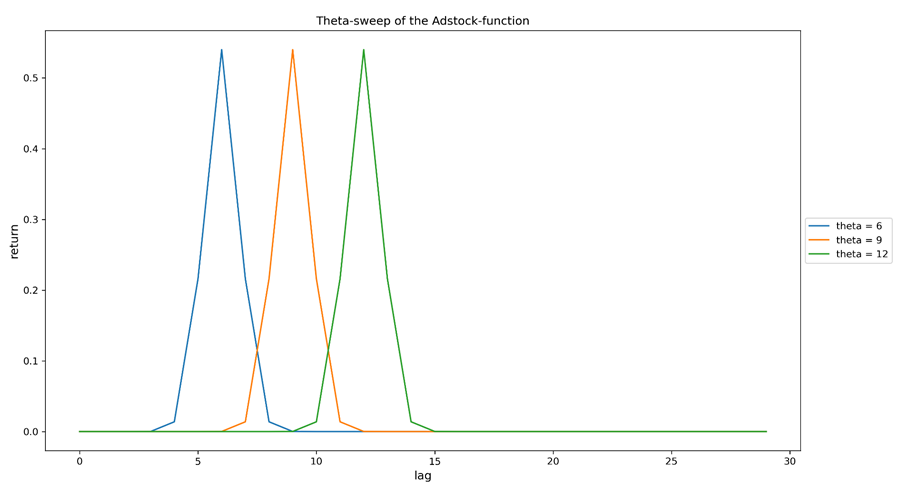
Figure 2a. Balayage du paramètre thêta (délai maximal) de la fonction Adstock. Toutes les courbes sont le résultat d'un investissement unique effectué au lag=0 (le lag peut indiquer n'importe quelle granularité temporelle choisie dans la modélisation). Plus le paramètre thêta est grand, plus il faut de temps pour que le revenu maximal soit observé, par rapport à l'investissement qui l'a provoqué.

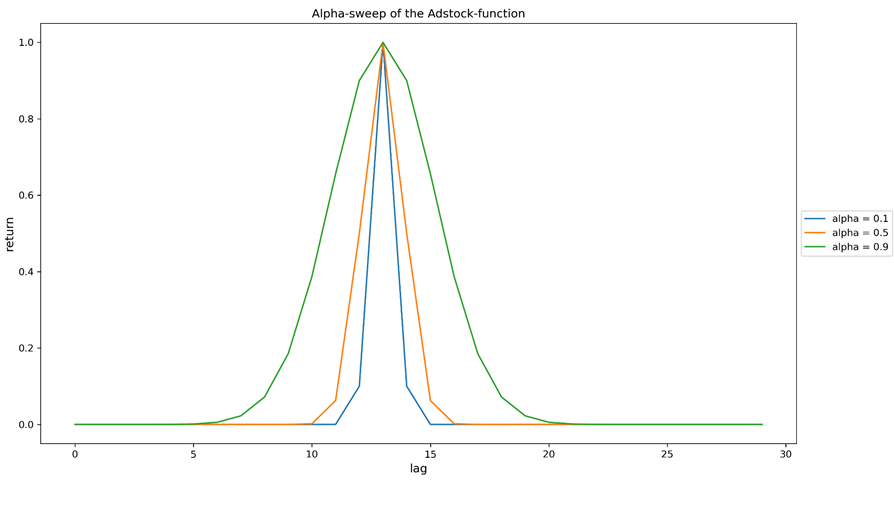
Figure 2b. Balayage du paramètre alpha (taux de rétention) de la fonction Adstock. Toutes les courbes sont le résultat d'un investissement unique effectué au lag=0 (le lag peut indiquer n'importe quelle granularité temporelle choisie dans la modélisation). Plus alpha est grand, plus la distribution des revenus est délocalisée. Les courbes ont été remises à l'échelle pour une meilleure comparaison.

Une fois que les deux mappings non linéaires et leurs paramètres respectifs sont définis, le modèle complet peut être donné comme suit :

Équation 4. Équation de régression de la modélisation du mix média

>Commençons notre analyse en décomposant l'expression ci-dessus. La première observation importante est que toutes les caractéristiques sont regroupées en investissements marketing et en variables externes (de contrôle), la différence la plus pertinente étant que les transformations de Hill et d'Adstock sont appliquées exclusivement aux premiers. Il convient donc de noter que l'impact des caractéristiques de contrôle est considéré comme purement linéaire et immédiat - même si les effets de tendance et de saisonnalité peuvent être ajoutés par le biais de caractéristiques de décalage et de saisonnalité, respectivement. Les variables de contrôle peuvent également être considérées comme l'ensemble des facteurs extérieurs au marketing qui ont un impact sur les ventes, y compris les prix, les ventes des concurrents, etc. Outre les termes de régression, nous tenons également compte d'un coefficient linéaire tau et d'un terme de bruit epsilon.

>Lorsque tout est inclus, cette formulation engendre 4 paramètres non linéaires pour chaque caractéristique marketing. En fonction du champ d'application du MMM et de la manière dont toutes les actions de marketing sont considérées, notre modèle peut nécessiter plusieurs caractéristiques de marketing différentes, ce qui rend le nombre de paramètres non linéaires très important. La façon dont ceux-ci sont traités dans la modélisation implique différentes stratégies possibles, comme nous le verrons dans ce qui suit.

Les lecteurs les plus perspicaces auront peut-être remarqué que les statistiques bayésiennes n'ont pas été évoquées une seule fois dans les sections précédentes. Cela soulève la question suivante : pourquoi devrions-nous nous intéresser à l'utilisation d'une approche bayésienne pour ajuster ce modèle, lorsqu'une observation spécifique data est disponible ?

Il s'avère que la réponse est très liée au grand nombre de paramètres qui doivent être approximés - un nombre qui est très souvent laissé de côté par la disponibilité de data pour s'adapter à notre modèle. Examinons la matrice Expertise x Data Availability ci-dessous :

Figure 4 :Matrice de disponibilité Expertise x Data pour l'étude Media Mix Modeling

Il ressort clairement de cette matrice que la complexité du problème à traiter ici dépend de la question suivante : l'approximation de tous ces paramètres non linéaires fait-elle partie de notre tâche ? Si ce n'est pas le cas - c'est-à-dire si ces paramètres sont déjà connus - ils ne devraient apparaître que comme des pré-transformations de data, qui seront ensuite intégrées dans un simple modèle de régression linéaire à plusieurs variables. C'est idéalement le cas si l'on dispose de suffisamment d'informations/expertises antérieures pour fixer des valeurs approximatives à ces paramètres, et que ces valeurs ne peuvent tout simplement pas être validées par data.

Il va sans dire que la connaissance absolue du comportement des canaux parmi tous les types de médias est une hypothèse assez forte, et qu'il y a de fortes chances que l'on dispose tout au plus de quelques indices concernant ces paramètres pour la modélisation. Par conséquent, l'observation data doit également être utilisée pour ajuster ces paramètres et mieux comprendre les canaux concernés. Si cela est associé à une faible disponibilité de data , il devient extrêmement pratique - voire nécessaire - d'utiliser toutes les informations précédemment connues afin de garantir une bonne performance du modèle.

L'approche bayésienne est donc un moyen d'effectuer une estimation tout-en-un des paramètres (régression et non linéaire), qui permet d'introduire des indices dans le modèle en tant que connaissances préalables, afin d'obtenir les meilleures performances avec un nombre limité de data. Entrons maintenant un peu plus dans les détails de la manière dont cela peut être réalisé.

Le MMM bayésien adapte un ensemble de distributions préalables (une pour la valeur de chaque paramètre linéaire ou non linéaire) en un ensemble de distributions postérieures. Cela se fait par l'exposition à data (preuves), et les distributions postérieures peuvent être considérées comme des interprétations révisées de la façon dont chaque canal se comporte et contribue aux ventes. En Python, cela peut être mis en œuvre avec des bibliothèques de modélisation probabiliste telles que PySTAN ou PyMC3.

Il convient de noter que cette stratégie ouvre un nouvel ensemble d'entrées contrôlables, autres que l'observation data: les distributions préalables. En effet, il existe une grande flexibilité dans le choix de la distribution pour chaque paramètre et dans l'adaptation de leurs moments en fonction de chaque canal, ce qui se traduira par un résultat différent pour la même observation data. Alors que l'article original de Google [1] fait état de distributions dont on a observé empiriquement qu'elles étaient plus performantes pour chaque type de paramètre(K, S, alpha, thêta et bêta), nous examinerons ici comment nous pouvons les adapter davantage à chaque canal individuel en fonction de nos connaissances antérieures sur leur comportement.

Avant d'examiner les distributions préalables pour chaque paramètre, une stratégie potentiellement utile à garder à l'esprit consiste à vérifier s'il n'est pas possible d'écarter complètement certains de ces paramètres. Cela nous aidera non seulement à simplifier le modèle, mais aussi (par conséquent) à obtenir de meilleures performances sur un nombre limité de sites data.

En effet, même s'il est démontré que les correspondances non linéaires s'appliquent à toutes les caractéristiques du marketing dans l'équation 4, il peut être judicieux d'écarter une ou les deux transformations pour certaines actions spécifiques : par exemple, si ces caractéristiques sont étendues aux actions commerciales et pas seulement aux canaux médiatiques, il peut être intéressant d'inclure les investissements dans la RPT (réduction temporaire des prix) en tant que caractéristique. Cela a un effet immédiat évident, car l'augmentation des ventes est observée et supprimée pratiquement au même moment que l'investissement (réduction de prix) démarre et s'accroît, respectivement. Il n'y a donc peut-être aucun intérêt à utiliser la transformation d'Adstock pour cette caractéristique, qui a l'avantage de réduire le nombre de paramètres à estimer.

Another viable simplification can be implemented for channels whose investments are known to vary very little in time: in these cases, we are operating at only a very small section of the curves shown in Figure 1, where the relation between return and investment can be deemed approximately linear. Hence, we can discard the Hill function for these channels, as saturation will not play an important role. In more technical terms, this assumption is valid when dx<<K, where dx is some measure of historical variation on investment.

Une fois que la pertinence de tous les paramètres non linéaires est vérifiée, l'étape suivante consiste à comprendre comment leurs antécédents peuvent être porteurs d'informations. Jusqu'à présent, j'ai volontairement utilisé le terme techniquement assez vague d'"indices" pour définir tout type d'entrée de modèle qui n'est pas une observation structurée sous forme de tableau data. Nous examinerons ici quelques exemples de ce qu'ils pourraient être et nous comblerons également le fossé entre ces indices et les distributions préalables réelles qui serviront d'entrée pour l'inférence bayésienne, en transportant ces connaissances dans le modèle.

Prenons tout d'abord l'exemple du prix par rapport à la concurrence. Il s'agit d'une variable externe qui, par nature, a un fort impact sur les ventes et qui pourrait donc être incluse comme élément de contrôle dans le modèle MMM. On pourrait facilement affirmer que plus ce prix relatif est élevé, plus les ventes seront faibles. Il s'agit là d'une question de bon sens, mais nous devrions explicitement indiquer au modèle de ne rechercher que des solutions ayant un impact négatif. Pour ce faire, nous choisissons une distribution préalable du paramètre bêta associé au prix (voir l'équation 4) qui soit une demi normale négative. Nous faisons l'inverse pour les caractéristiques ayant un impact positif (par exemple, si vous modélisez des ventes de boissons rafraîchissantes, la température moyenne hebdomadaire doit avoir un impact positif). Notez que ce n'est pas une nécessité : si vous n'êtes pas tout à fait sûr de l'impact d'une caractéristique sur la variable cible, vous pouvez lui donner un a priori non informé (par exemple, la distribution normale standard) et laisser le modèle l'apprendre par lui-même.

Il ne s'agit là que d'un exemple de la manière d'ajuster les distributions préalables afin d'inclure des connaissances qualitatives dans le modèle. D'autres informations qualitatives peuvent provenir, par exemple, de la nature d'une action de marketing spécifique (comme dans l'exemple précédent pour le TPR, si l'on décide de ne pas réduire complètement le délai, mais plutôt de modifier sa distribution pour se concentrer uniquement sur les délais très courts). Les connaissances quantitatives préalables, quant à elles, peuvent provenir d'études ou d'estimations antérieures réalisées sur la base d'une analyse historique ( data ). Dans le premier cas, la distribution des poids de régression peut être décalée en fonction de la valeur du retour sur investissement qui a été trouvée dans une étude MMM antérieure - le modèle peut alors rechercher des valeurs plus petites/élevées dès le départ, pour les canaux dont on sait qu'ils ont des rendements plus petits/plus grands ; dans le second cas, l'hypothèse selon laquelle les investissements historiques devraient être à peu près du même ordre que le niveau d'investissement idéal peut conduire à des connaissances préalables sur le paramètre de saturation K de l'équation 1 - le modèle est ainsi informé des canaux qui sont plus grands ou plus petits en termes de portée potentielle.

La matrice ci-dessous résume certaines stratégies clés qui peuvent être envisagées pour ajuster les distributions préalables, tant qualitatives que quantitatives. Il ne s'agit en aucun cas d'une liste exhaustive, et la viabilité de chacune d'entre elles peut varier en fonction du contexte et doit être revue pour chaque étude spécifique.

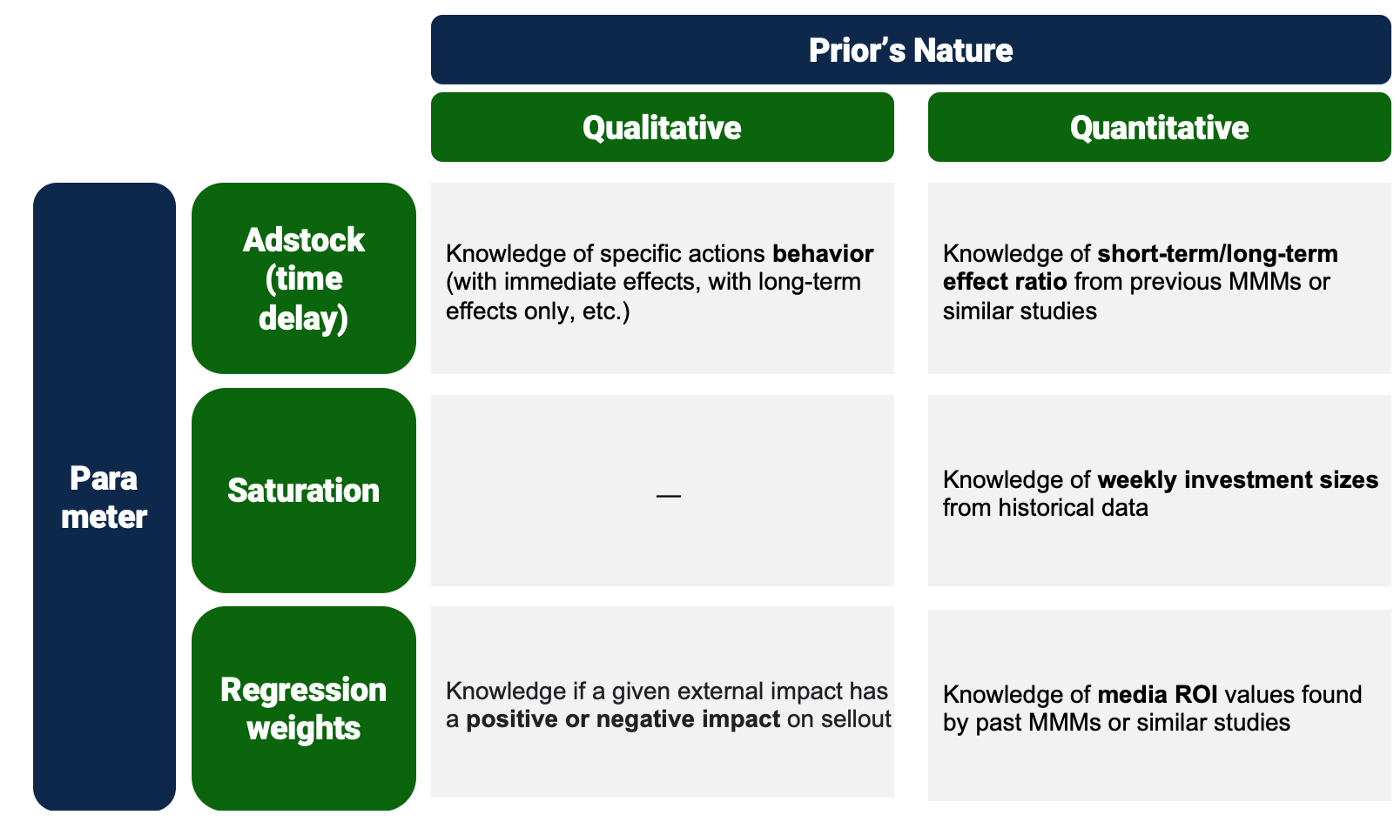
Figure 5. Exemple de matrice de stratégie d'accord préalable pour un cas d'utilisation de la modélisation bayésienne du mix média. Les stratégies devraient varier en fonction du champ d'application et des connaissances actuelles disponibles.

Alors qu'une étude de modélisation du mix média nécessite de traiter le comportement de plusieurs actions marketing différentes, l'approche bayésienne permet une estimation globale de ces actions, ainsi que de l'augmentation des ventes pour chacune de ces caractéristiques ainsi que pour des facteurs externes (caractéristiques de contrôle). Cela nous permet d'exploiter les observations disponibles sur data afin d'apprendre ces comportements lorsqu'ils ne sont pas connus à l'avance grâce à l'expertise disponible ou à des études et des tests antérieurs spécifiques au canal. Néanmoins, cela a un coût, qui se reflète principalement dans la complexité du modèle et dans le besoin subséquent d'un nombre suffisant de sites data pour obtenir de bonnes performances. Lorsque ce besoin n'est pas satisfait, le principal résultat est un modèle qui peut facilement suradapter le site data observé en donnant des paramètres qui ne sont tout simplement pas raisonnables.

Dans cet article, nous avons exploré un moyen de remédier à cet effet en travaillant avec des connaissances antérieures autres que les données observables data, qu'il s'agisse de conclusions quantitatives d'études antérieures ou d'une compréhension qualitative par les entreprises de la nature d'une caractéristique et de son impact sur les ventes. Ces connaissances sont prises en compte en adaptant les distributions préalables de chacun des paramètres du modèle. Si, d'un point de vue pragmatique, on peut considérer que cela biaise le modèle, c'est aussi un moyen d'éviter de surajuster le modèle à des modèles qui ne sont observés qu'en raison de la disponibilité limitée du site data, en se concentrant sur des combinaisons qui sont proches de ce que l'on sait ou du moins de ce que l'on s'attend à ce qu'elles soient vraies. En d'autres termes, l'adaptation des distributions est un moyen de faire un compromis entre l'apprentissage à partir de nouvelles observations data et le respect des anciennes connaissances commerciales - un compromis qui peut être exploré à plusieurs niveaux différents en fonction de ce qui est disponible dans un cas spécifique de modélisation du mixage des médias.

Nous remercions tout particulièrement Camila C. Moreno, Rafael Melo, Rhayssa Sonohata, Vinicius Pacheco et Wedeueis Braz de l'équipe brésilienne pour la relecture de cet article avant sa publication. Artefact pour avoir relu cet article avant sa publication.

[1] Jin, Y., Wang, Y., Sun, Y., Chan, D. et Koehler, J. (2017). Méthodes bayésiennes pour la modélisation du mix média avec des effets de report et de forme.