Bayesiaanse mediamixmodellering met beperkte data

Als je al eens te maken hebt gehad met MMM-problemen (Media Mix Modeling) in marketing, dan weet je misschien dat het hierbij gaat om een hele reeks kanaalspecifieke effecten (vertragingen, verzadiging en langetermijneffecten) die elk worden gemodelleerd via ten minste één verschillende parameter. Je weet misschien ook dat dit niet bepaald een context is waarin een overvloed aan data en/of data variabiliteit om je model te trainen gegarandeerd is. In klassieke MMM's zijn eerdere aannames over het gedrag van mediakanalen (d.w.z. over waarden voor de eerder genoemde parameters) nodig om de bijdrage van elk kanaal aan de verkoop te beoordelen via lineaire regressie. Een krachtig alternatief hiervoor is de Bayesiaanse MMM-benadering [1], die een alles-in-één schatting van zowel kanaalgedrag als omzetverhoging mogelijk maakt door middel van prior-distributies en data. Dit betekent dat onjuiste en onveranderlijke aannames worden vermeden als er in het verleden geen kanaalspecifieke studies zijn uitgevoerd. Uiteraard maakt dit het model ook veel complexer en wordt het invoeren van allerlei informatie die kan helpen bij het vinden van een goede oplossing cruciaal.

Er schuilt inderdaad een inherent gevaar in het louter laten vertrouwen van zo'n complex model op een beperkte data om te leren: in tegenstelling tot de meeste toepassingen van regressieproblemen moet een MMM-model eerder een beschrijvend dan een voorspellend hulpmiddel zijn. Een goede fit met de training data en generalisatie naar ongeziene data zijn dus interessant, maar niet genoeg: het moet ook correct inzicht geven in de werkelijke historische omzetstijging, return over investment(ROI) en verzadiging voor elk kanaal, om een betrouwbare output te garanderen voor het plannen van marketingstrategieën. Met andere woorden, het gevaar schuilt in het bestaan van verschillende parametercombinaties die correct passen bij de data, aangezien ze niet allemaal echt zinvol zijn - men zou kunnen stellen dat dit gewoon een andere manifestatie is van de vloek van de dimensionaliteit.

Maar wat betekent het voor een oplossing om "echt zinvol" te zijn? Een haalbaar antwoord is dat het model weliswaar vrij moet zijn om nieuwe patronen te leren van data, maar dat de output niet volledig mag afwijken van eerdere bedrijfskennis die mogelijk beschikbaar is. De mogelijkheid om deze informatie op te nemen als voorkennis (zodat we het model kunnen helpen bij het vinden van een verstandige parametercombinatie) is slechts een van de veelzijdige en krachtige aspecten van de Bayesiaanse oplossing.>

In dit artikel bekijken we hoe kwalitatieve en kwantitatieve bedrijfskennis kan worden vertaald naar op maat gemaakte prior verdelingen die een goed presterende MMM mogelijk maken, zelfs als informatie via gestructureerde historische data schaars is.

Voordat we onderzoeken hoe we kansverdelingen kunnen gebruiken om de prestaties van ons model te optimaliseren, beginnen we met enkele belangrijke definities voor de Media Mix Modeling zelf. In essentie is de MMM gebaseerd op een lineaire regressie, waarbij de afhankelijke variabele de doelomzet is en de onafhankelijke variabelen (kenmerken) de investering in verschillende marketingacties zijn, evenals externe controlevariabelen die ook invloed hebben op de omzet (prijs, concurrentie, seizoensgebondenheid, enz.).

Er is echter een cruciaal verschil tussen deze formulering en die van een conventioneel lineair regressiemodel: De kenmerken van marketinginvesteringen moeten ook een reeks niet-lineaire transformaties ondergaan, die in de eerste plaats bedoeld zijn om het verwachte gedrag van mediakanalen weer te geven dat niet via lineaire koppelingen kan worden gemodelleerd. Deze transformaties hebben elk een subset van parameters die de algemene intensiteit en aard van deze gedragingen bepalen. Er zijn twee belangrijke niet-lineaire transformaties, verzadiging en tijdvertraging, die in wat volgt kort zullen worden behandeld.

Verzadiging is een zeer bekend effect op marketingkanalen, dat zich vertaalt in een niet-lineaire relatie tussen de investering en de daaruit voortvloeiende inkomsten. Dit kan worden begrepen als het effect van advertenties die naar steeds minder relevante gebruikers worden gebracht, of als gevolg van de relatief kleinere toename in bereik (nieuwe blootgestelde gebruikers) met elke extra geïnvesteerde dollar. Het verzadigingseffect kan worden gemodelleerd via de Hill-vergelijking hieronder. Omdat de exacte uitdrukking hier niet echt van belang is, wordt de lezer uitgenodigd zich te concentreren op figuur 1a en 1b, die laten zien wat er gebeurt met de Hill-functie als de waarden van de twee parameters worden gewijzigd.

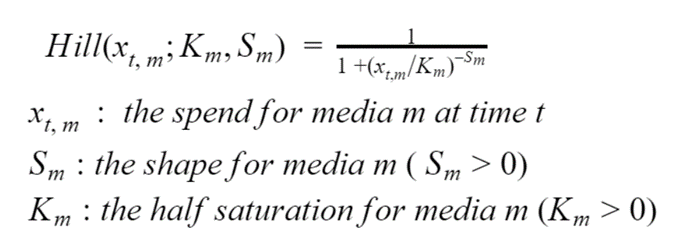
Vergelijking 1. De Hill-vergelijking

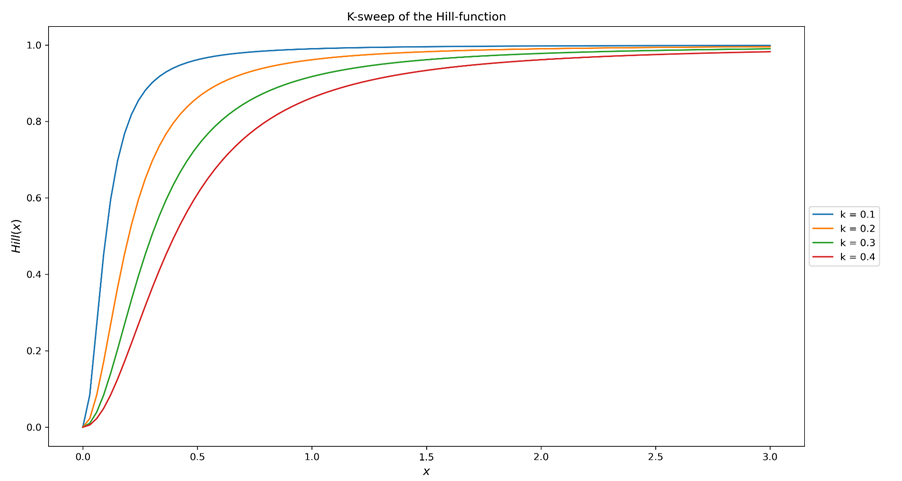
Figuur 1a. Het verschuiven van de K-parameter (halfverzadiging) van de Hill-functie. De algemene vorm van de curve blijft ongeveer behouden, terwijl het punt van halve verzadiging (waar Hill(x)=0,5) wordt verschoven. Met andere woorden, hoe groter K is, hoe moeilijker het is om het bijbehorende mediakanaal te verzadigen.

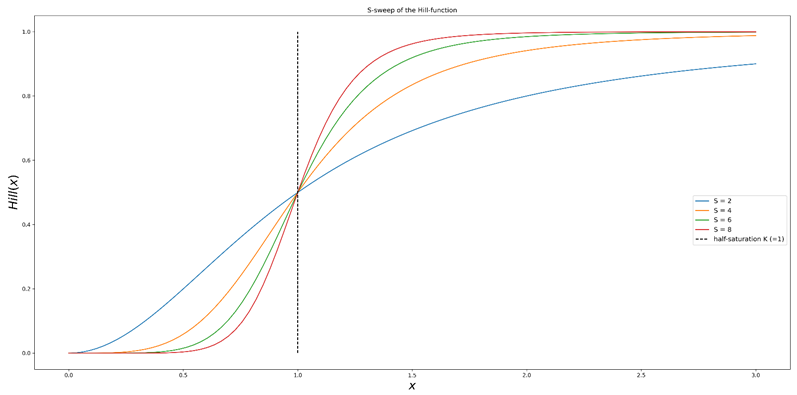
Figuur 1b. Het vegen van de S-parameter (vorm) van de Hill-functie. Het halfverzadigingspunt van de curve blijft behouden terwijl de helling eromheen toeneemt. Met andere woorden, hoe groter S is, hoe groter de marginale winst voor investeringen rond het halve verzadigingspunt.

Zoals hierboven is aangetoond, bevat de Hill-vergelijking twee belangrijke parameters: terwijl K het punt van halfverzadiging bepaalt (het kanaal is precies op de helft van zijn maximale inkomsten als de investering gelijk is aan K), beïnvloedt S de vorm van de verzadigingscurve (hoe hoger de waarde, hoe S-vormiger de curve wordt). Het leren van nauwkeurige schattingen voor K en S is essentieel omdat een optimaal investeringsniveau analytisch uit deze parameters kan worden afgeleid. Immers, wanneer er geen ander effect wordt overwogen, kan de investering die een maximale Return over Investment (ROI) oplevert als volgt worden berekend:

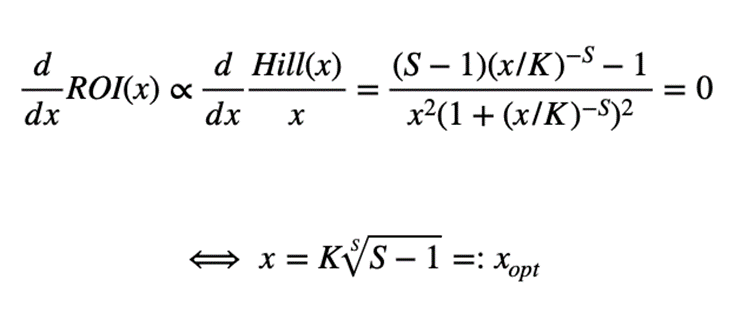
Vergelijking 2. Het optimale investeringsniveau afleiden uit verzadigingsparameters

Merk op dat deze optimale investering bestaat voor S>1 en dat deze altijd tussen één en drie keer de halfverzadigingswaarde K ligt (je kunt dit controleren door de waarden na te gaan die de S-wortel kan aannemen).

Het tweede effect waar rekening mee moet worden gehouden is de tijdsallocatie van de inkomsten, nadat bepaalde kanaalspecifieke investeringen zijn gedaan. Investeringen en inkomsten vinden namelijk niet gelijktijdig plaats, en het kan een paar weken duren voordat de laatste significant wordt. Bovendien zullen sommige mediakanalen meer gelokaliseerde effecten hebben, terwijl andere kanalen investeringen langer kunnen vasthouden en zo zelfs na relatief lange perioden inkomsten genereren. Beide aspecten kunnen worden gemodelleerd via de Adstock-vergelijking hieronder, door respectievelijk de theta- en alpha-parameters. De L-parameter hoeft niet specifiek te zijn voor elk kanaal en kan alleen worden ingesteld op een vaste waarde waarvan empirisch bekend is dat deze voldoende groot is, zoals L=13 (zoals voorgesteld in [1]). Nogmaals, de lezer wordt uitgenodigd zich te concentreren op figuren 2a en 2b in plaats van op vergelijking 3.

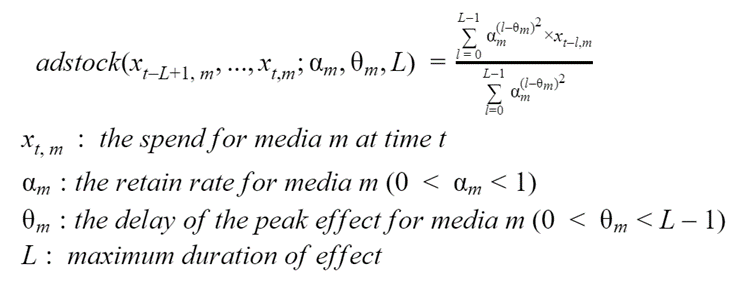
Vergelijking 3. De Adstock-vergelijking

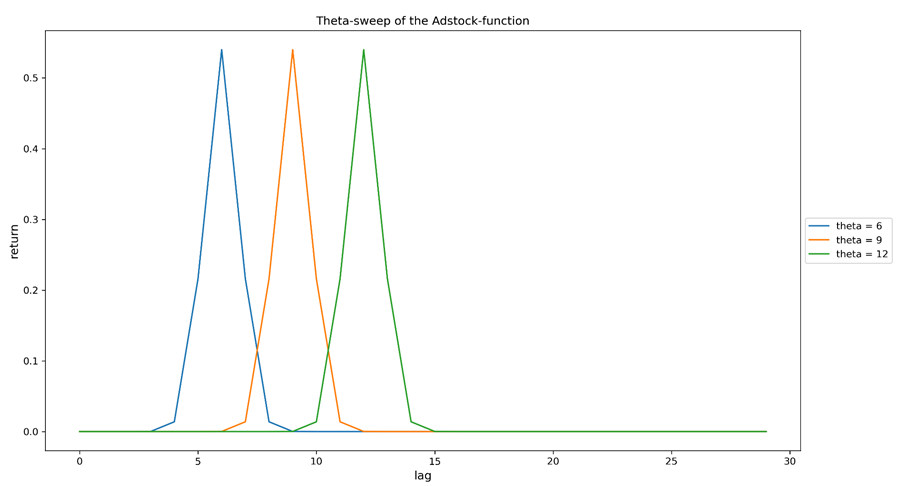
Figuur 2a. Het vegen van de theta-parameter (piekvertraging) van de Adstock-functie. Alle curven zijn het resultaat van een enkele investering die is gedaan op lag=0 (lag kan een willekeurige tijdkorrelgrootte zijn die is gekozen bij het modelleren). Hoe groter theta is, hoe langer het duurt voordat de maximale opbrengst wordt waargenomen, in relatie tot de investering die deze heeft veroorzaakt.

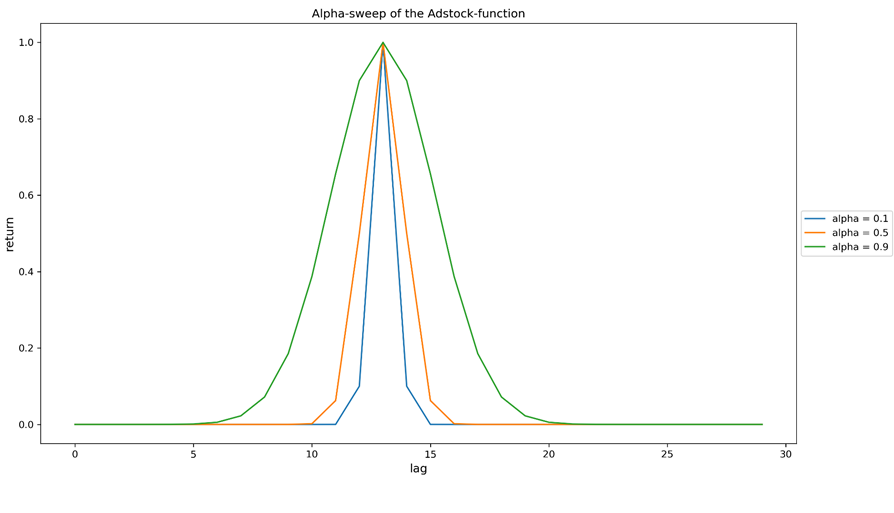
Afbeelding 2b. Het vegen van de alpha-parameter (behoudsnelheid) van de Adstock-functie. Alle curven zijn het resultaat van een enkele investering die is gedaan op lag=0 (lag kan een willekeurige tijdkorrelgrootte zijn die is gekozen bij het modelleren). Hoe groter alpha is, hoe meer gedelokaliseerd de inkomstenverdeling is. De curven zijn herschaald voor een betere vergelijking.

Zodra beide niet-lineaire koppelingen en hun respectievelijke parameters gedefinieerd zijn, kan het volledige model als volgt gegeven worden:

Vergelijking 4. Media Mix Modellering regressievergelijking

>Laten we beginnen met onze analyse door de bovenstaande uitdrukking uit te splitsen. De eerste belangrijke observatie is dat alle kenmerken zijn geclusterd in marketinginvesteringen en externe (controle)variabelen, met als meest relevante verschil dat de Hill en Adstock transformaties alleen worden toegepast op de eerstgenoemde. Merk dus op dat het effect van controlekenmerken als zuiver lineair en onmiddellijk wordt beschouwd, ook al kunnen trend- en seizoensgebonden effecten worden toegevoegd door respectievelijk vertragings- en seizoensgebonden kenmerken. Controlevariabelen kunnen ook worden beschouwd als de verzameling factoren buiten Marketing die van invloed zijn op de verkoop, waaronder prijsstelling, verkoop van concurrenten, enz. Naast de regressietermen houden we ook rekening met een lineaire coëfficiënt tau en een ruisterm epsilon.

>Als alles wordt meegenomen, levert deze formulering 4 niet-lineaire parameters op voor elk marketingkenmerk. Afhankelijk van de reikwijdte van de MMM en van hoe specifiek alle marketingacties worden beschouwd, kan ons model verschillende marketingkenmerken vereisen, waardoor het aantal niet-lineaire parameters erg belangrijk wordt. De manier waarop deze worden behandeld in de modellering impliceert verschillende mogelijke strategieën, zoals in wat volgt zal worden besproken.

De meest opmerkzame lezers hebben misschien gemerkt dat de Bayesiaanse statistiek niet één keer is genoemd in de vorige hoofdstukken. Dit roept de vraag op: waarom zouden we ons druk maken over het gebruik van een Bayesiaanse benadering voor het passen van dit model, als er een specifieke observatie data beschikbaar is?

Het antwoord blijkt nauw samen te hangen met het grote aantal parameters dat moet worden benaderd - een aantal dat vaak niet wordt geëvenaard door de data beschikbaarheid om in ons model te passen. Laten we eens kijken naar de onderstaande Expertise x Data beschikbaarheidsmatrix:

Figuur 4.Expertise x Data Beschikbaarheid matrix voor de Media Mix Modeling studie

Uit deze matrix moet duidelijk worden dat de complexiteit van het probleem dat hier moet worden aangepakt, afhangt van de volgende vraag: maakt het benaderen van al deze niet-lineaire parameters deel uit van onze taak? Zo niet - dat wil zeggen, als deze parameters al eerder bekend zijn - dan moeten ze alleen verschijnen als voorvervormingen op de data, die dan worden ingepast in een eenvoudig lineair multivariaat regressiemodel. Dit is idealiter het geval als er voldoende informatie/expertise uit het verleden beschikbaar is om benaderende waarden voor deze parameters vast te stellen en deze waarden eenvoudigweg niet kunnen worden gevalideerd door data.

Het behoeft geen betoog dat de absolute kennis van het kanaalgedrag van alle mediatypen nogal een sterke aanname is, en de kans is groot dat er hooguit enkele aanwijzingen met betrekking tot deze parameters beschikbaar zijn voor modellering. Daarom moet de observatie data ook gebruikt worden om deze parameters te fitten en de betrokken kanalen beter te begrijpen. Als dit gepaard gaat met een lage beschikbaarheid van data , wordt het erg handig - of zelfs verplicht - om alle eerder bekende informatie te gebruiken om goede modelprestaties te garanderen.

De Bayesiaanse benadering is dus een manier om een alles-in-een schatting van parameters uit te voeren (regressie en niet-lineair), die het mogelijk maakt om aanwijzingen in het model in te voeren als voorkennis, voor de beste prestaties met beperkte data. Laten we nu wat dieper ingaan op de details over hoe dit kan worden bereikt.

De Bayesiaanse MMM past een reeks prior-verdelingen (één voor de waarde van elke lineaire of niet-lineaire parameter) aan in een reeks posterior-verdelingen. Dit wordt gedaan door de blootstelling aan data (bewijs), en de posterior verdelingen kunnen worden beschouwd als een herzien begrip van hoe elk kanaal zich gedraagt en bijdraagt aan de verkoop. In Python kan dit worden geïmplementeerd met probabilistische modelleerbibliotheken zoals PySTAN of PyMC3.

Merk op dat deze strategie een nieuwe reeks beheersbare inputs opent, anders dan observatie data: de prior-verdelingen. Er is namelijk veel flexibiliteit in de keuze van verdelingen voor elke parameter en in het aanpassen van hun momenten aan elk kanaal, wat dan resulteert in een andere uitvoer voor dezelfde observatie data. Terwijl het oorspronkelijke Google-artikel [1] reports verdelingen bevat waarvan empirisch is vastgesteld dat ze beter presteren voor elk parametertype(K, S, alfa, theta en bèta), zullen we hier onderzoeken hoe we deze verdelingen verder kunnen afstemmen op elk afzonderlijk kanaal op basis van eerdere kennis over hun gedrag.

Voordat we ons gaan verdiepen in prior-verdelingen voor elke parameter, is een mogelijk nuttige strategie om in gedachten te houden om te controleren of we sommige van deze parameters niet helemaal kunnen weglaten. Dit zal ons niet alleen helpen om het model te vereenvoudigen, maar ook (als gevolg daarvan) om betere prestaties te verkrijgen in beperkte data.

Inderdaad, ook al is aangetoond dat de niet-lineaire mappings worden toegepast op alle Marketing kenmerken in vergelijking 4, kan het ook verstandig zijn om een of beide transformaties weg te gooien voor een aantal specifieke acties: bijvoorbeeld, als deze functies worden uitgebreid tot de handel acties en niet alleen mediakanalen, kan men geïnteresseerd zijn in het opnemen van TPR (Tijdelijke Prijsverlaging) investeringen als een kenmerk. Dit heeft een duidelijk onmiddellijk effect, omdat de verkoop lift wordt waargenomen en gedood op vrijwel hetzelfde moment als de investering (prijsverlaging) begint en beslag legt, respectievelijk. Daarom is het misschien niet interessant om de Adstock-transformatie voor dit kenmerk te gebruiken, wat als voordeel heeft dat het aantal te schatten parameters wordt verminderd.

Another viable simplification can be implemented for channels whose investments are known to vary very little in time: in these cases, we are operating at only a very small section of the curves shown in Figure 1, where the relation between return and investment can be deemed approximately linear. Hence, we can discard the Hill function for these channels, as saturation will not play an important role. In more technical terms, this assumption is valid when dx<<K, where dx is some measure of historical variation on investment.

Zodra de relevantie van alle niet-lineaire parameters is geverifieerd, is de volgende stap om te begrijpen hoe hun prioriteiten informatie kunnen dragen. Tot nu toe heb ik met opzet de nogal technisch vage term "aanwijzingen" gebruikt om elke vorm van modelinvoer te definiëren die geen gestructureerde, tabelachtige waarneming is data. Hier zullen we enkele voorbeelden bekijken van wat deze zouden kunnen zijn en ook de kloof dichten tussen deze en de werkelijke prior-verdelingen die als input dienen voor de Bayesiaanse inferentie, waarbij deze kennis in het model wordt gebracht.

Laten we eerst het voorbeeld nemen van de prijs ten opzichte van de concurrentie. Dit is een externe variabele die inherent een sterke invloed heeft op de verkoop en dus als een controlefunctie zou kunnen worden opgenomen in het MMM-model. Je zou gemakkelijk kunnen stellen dat hoe hoger deze relatieve prijs is, hoe lager de verkoop zal zijn. Dit lijkt ons logisch, maar we moeten het model expliciet vertellen dat het alleen moet zoeken naar oplossingen met een negatieve impact. De manier waarop we dit doen is door te kiezen dat de prior-verdeling voor de parameter bèta geassocieerd met prijs (zie Vergelijking 4) een negatieve halfnormale verdeling is. We doen het tegenovergestelde voor kenmerken met een positieve impact (bijv. als u de verkoop van verfrissende dranken modelleert, zou de wekelijkse gemiddelde temperatuur een positieve impact moeten hebben). Merk op dat dit niet noodzakelijk is: als u niet helemaal zeker bent van de impact van een kenmerk op de doelvariabele, kunt u het een ongeïnformeerde prior geven (bijvoorbeeld de standaard normale verdeling) en het model dit zelf laten leren.

Dit is slechts een voorbeeld van hoe je priorverdelingen kunt afstemmen om kwalitatieve kennis in het model op te nemen. Andere mogelijke kwalitatieve informatie kan bijvoorbeeld afkomstig zijn van een specifieke marketingactie (zoals in het eerder gegeven voorbeeld voor TPR, als men besluit om de tijdvertraging niet helemaal te verkorten, maar de verdeling te verschuiven zodat deze zich alleen concentreert op zeer korte vertragingen). Kwantitatieve voorkennis, aan de andere kant, kan afkomstig zijn van eerdere studies of schattingen uitgevoerd op historische data analyse. Als voorbeeld voor het eerste kan de verdeling van het regressiegewicht worden verschoven in overeenstemming met de ROI-waarde die werd gevonden in een eerdere MMM-studie - het model kan dan vanaf het begin zoeken naar kleinere/hogere waarden voor kanalen waarvan bekend is dat ze kleinere/grotere rendementen hebben; wat betreft het laatste kan de aanname dat historische investeringen ongeveer van dezelfde orde moeten zijn als het ideale investeringsniveau leiden tot geïnformeerde voorkennis over de verzadigingsparameter K uit vergelijking 1 - het model weet dus welke kanalen groter of kleiner zijn in termen van potentieel bereik.

De matrix hieronder geeft een overzicht van enkele belangrijke strategieën die overwogen kunnen worden voor het afstemmen van priorverdelingen, zowel kwalitatief als kwantitatief. Dit is zeker geen uitputtende lijst en de haalbaarheid van elke strategie kan variëren afhankelijk van de context en moet voor elk specifiek onderzoek worden herzien.

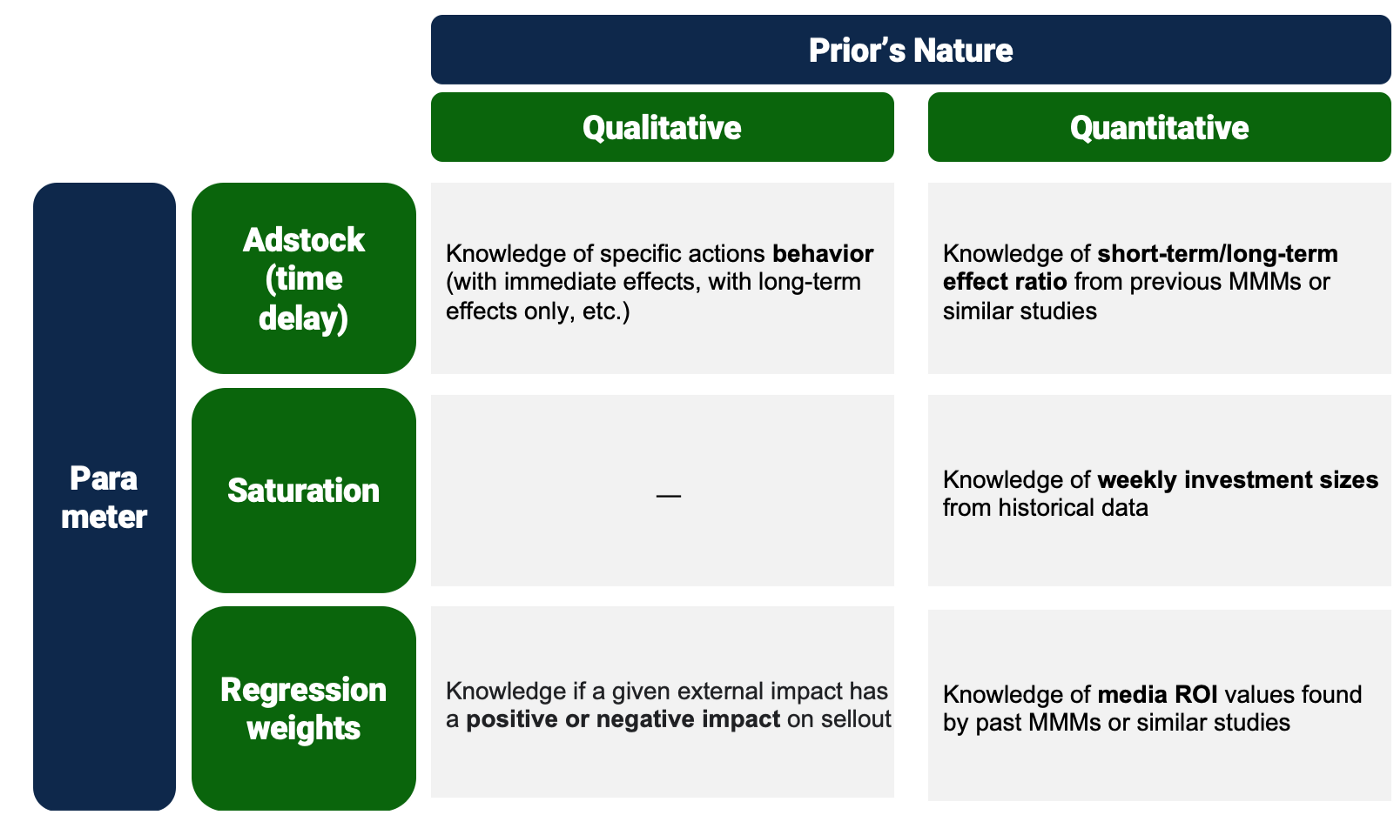
Figuur 5. Voorbeeld van een prior tuning strategiematrix voor een use-case van de Bayesiaanse mediamixmodellering. Strategieën moeten variëren afhankelijk van de reikwijdte en beschikbare huidige kennis

Terwijl een Media Mix Modeling-studie te maken heeft met het gedrag van verschillende marketingacties, maakt de Bayesiaanse benadering een alles-in-één schatting hiervan mogelijk, naast de omzetstijging voor elk van deze kenmerken en voor externe factoren (controlekenmerken). Dit stelt ons in staat om de beschikbare geobserveerde data te oogsten om dit gedrag te leren wanneer het niet vooraf bekend is via beschikbare expertise of kanaalspecifieke onderzoeken en tests uit het verleden. Hier hangt echter een prijskaartje aan, dat vooral tot uiting komt in de complexiteit van het model en de daaruit voortvloeiende behoefte aan voldoende data om een goede prestatie te leveren. Als niet aan deze behoefte wordt voldaan, is een van de belangrijkste resultaten een model dat vrij gemakkelijk kan overpassen op de waargenomen data door parameters op te geven die gewoonweg niet redelijk zijn.

In dit artikel hebben we een manier onderzocht om dit effect te verhelpen door te werken met andere eerdere kennis dan waarneembare data, van kwantitatieve conclusies in eerdere onderzoeken tot kwalitatieve zakelijke inzichten in de aard van bepaalde kenmerken en de invloed ervan op de verkoop. Deze worden meegenomen door de prior verdelingen van elk van de parameters van het model aan te passen. Vanuit pragmatisch oogpunt kan dit worden opgevat als het beïnvloeden van het model, maar het is ook een manier om te voorkomen dat het model te veel past bij patronen die alleen worden waargenomen omdat de databeperkt beschikbaar is, door te focussen op combinaties die dicht liggen bij wat bekend is of waarvan op zijn minst wordt verwacht dat ze waar zijn. Met andere woorden, het op maat maken van verdelingen is een manier om een compromis te sluiten tussen leren van nieuwe waarnemingen data en het respecteren van oude bedrijfskennis - een compromis dat op verschillende niveaus kan worden onderzocht, afhankelijk van wat beschikbaar is in een specifieke casus voor mediamixmodellering.

Speciale dank aan Camila C. Moreno, Rafael Melo, Rhayssa Sonohata, Vinicius Pacheco en Wedeueis Braz van het Braziliaanse Artefact team voor het beoordelen van dit artikel voor publicatie.

[1] Jin, Y., Wang, Y., Sun, Y., Chan, D., & Koehler, J. (2017). Bayesiaanse methoden voor mediamixmodellering met carryover- en vormeffecten.