Modelización bayesiana de la combinación de medios con data

Si ya se ha enfrentado a problemas de modelado de combinación de medios (MMM) en marketing, sabrá que implican toda una serie de efectos específicos del canal (retrasos, saturación y efectos a largo plazo) que se modelan mediante al menos un parámetro diferente. También puede que sepa que éste no es precisamente un contexto en el que esté garantizada la abundancia de data y/o data variabilidad para entrenar su modelo. En los MMM clásicos, se requieren supuestos previos sobre el comportamiento de los canales de medios (es decir, sobre los valores de los parámetros mencionados) para evaluar la contribución de cada canal a las ventas mediante regresión lineal. Una potente alternativa a esto es el enfoque Bayesiano MMM [1], que permite una estimación todo-en-uno tanto del comportamiento del canal como de la elevación de las ventas a través de distribuciones a priori y data. Esto significa evitar suposiciones incorrectas e inmutables si no se han realizado estudios previos específicos del canal. Huelga decir que también hace que el modelo sea mucho más complejo, y que la introducción de todo tipo de información que pueda ayudar a encontrar una buena solución se convierte en algo crucial.

De hecho, existe un peligro inherente en dejar que un modelo tan complejo dependa puramente de la limitada data para aprender: al contrario que la mayoría de las aplicaciones de problemas de regresión, un modelo MMM debería funcionar como una herramienta descriptiva más que predictiva. Por lo tanto, un buen ajuste al entrenamiento data y la generalización a data son interesantes, pero no suficientes: también debe proporcionar información correcta sobre el aumento histórico real de las ventas, el retorno de la inversión(ROI) y la saturación de cada canal, con el fin de garantizar un resultado fiable para la planificación de estrategias de marketing. En otras palabras, el peligro reside en la existencia de varias combinaciones de parámetros que se ajusten correctamente a data, dado que no todas ellas tienen un sentido real; se podría argumentar que se trata de otra manifestación de la Maldición de la Dimensionalidad.

Pero, ¿qué significa que una solución tenga "sentido real"? Una respuesta viable es que, aunque el modelo debe tener libertad para aprender nuevos patrones a partir de data, su resultado no debe desviarse por completo de los conocimientos empresariales previos de que pueda disponer. De hecho, poder incluir esta información como conocimiento previo (de modo que podamos ayudar al modelo a encontrar una combinación de parámetros sensata) es sólo uno de los aspectos versátiles y potentes de la solución bayesiana.>

En este artículo, analizaremos cómo el conocimiento cualitativo y cuantitativo del negocio puede traducirse en distribuciones a priori a medida que harán posible un MMM de buen rendimiento incluso cuando la información a través del histórico estructurado data es escasa.

Antes de explorar cómo podemos aprovechar las distribuciones de probabilidad para optimizar el rendimiento de nuestro modelo, empecemos con algunas definiciones clave del propio Modelo de Combinación de Medios. En esencia, el MMM se basa en una regresión lineal, en la que la variable dependiente son las ventas objetivo y las variables independientes (características) son la inversión en diferentes acciones de marketing, así como variables de control externas que también influyen en las ventas (precios, competencia, estacionalidad, etc.).

No obstante, existe una diferencia crucial entre esta formulación y la de un modelo de regresión lineal convencional: Las características de la inversión en marketing también deben pasar por un conjunto de transformaciones no lineales, cuyo objetivo principal es representar los comportamientos esperados de los canales de los medios de comunicación que no pueden modelarse mediante mapeos lineales. Cada una de estas transformaciones conlleva un subconjunto de parámetros que controlan la intensidad y la naturaleza general de estos comportamientos. Hay dos transformaciones no lineales principales, la saturación y el retardo, que se tratarán brevemente a continuación.

La saturación es un efecto muy conocido en los canales de marketing, que se traduce en una relación no lineal entre la inversión y los ingresos generados. Puede entenderse como el efecto de que los anuncios lleguen a usuarios cada vez menos relevantes o, alternativamente, debido al aumento relativamente menor del alcance (nuevos usuarios expuestos) con cada dólar invertido adicional. El efecto de saturación puede modelizarse mediante la ecuación de Hill que se describe a continuación. Como la expresión exacta no es del todo de interés aquí, se invita al lector a centrarse en las figuras 1a y 1b, que muestran lo que ocurre con la función de Hill cuando se barren los valores de sus dos parámetros.

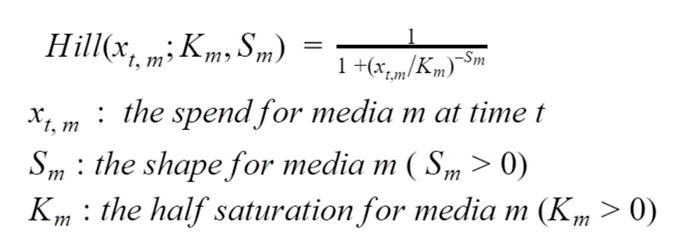
Ecuación 1. La ecuación de Hill

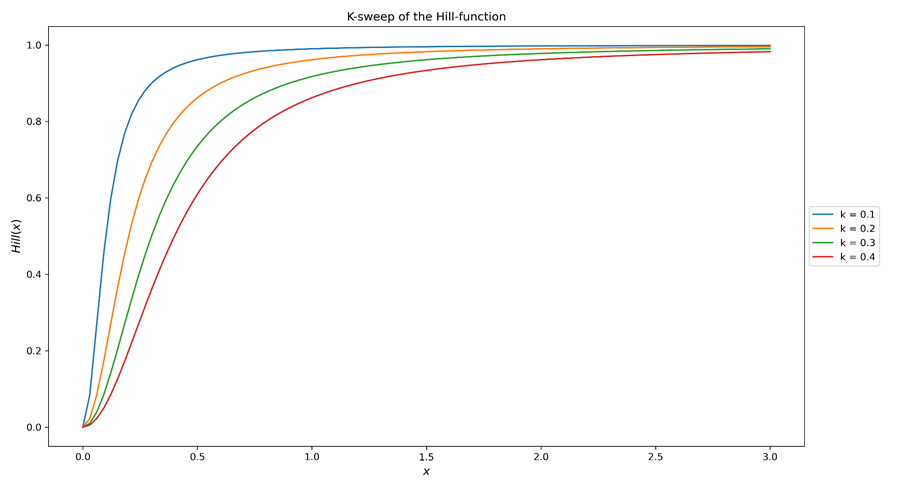
Figura 1a. Barrido del parámetro K (semisaturación) de la función de Hill. La forma general de la curva se mantiene aproximadamente, mientras que el punto de media saturación (donde Hill(x)=0,5) se desplaza. En otras palabras, cuanto mayor sea K, más difícil será saturar el canal de medios asociado.

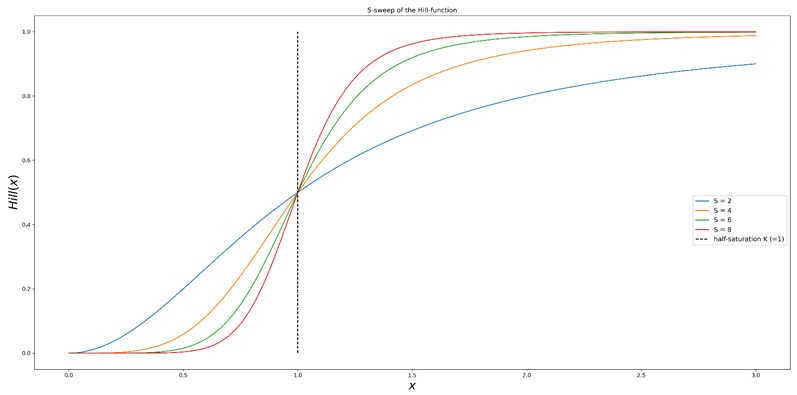
Figura 1b. Barrido del parámetro S (forma) de la función de Hill. El punto de semisaturación de la curva se mantiene, mientras que la pendiente a su alrededor aumenta. En otras palabras, cuanto mayor es S, mayores son las ganancias marginales de las inversiones en torno al punto de semisaturación.

Como se ha visto anteriormente, la ecuación de Hill contiene dos parámetros importantes: mientras que K define el punto de semisaturación (el canal está exactamente a la mitad de sus ingresos máximos cuando la inversión es igual a K), S interfiere en la forma de la curva de saturación (cuanto mayor sea su valor, más forma de S tendrá la curva). Es esencial obtener estimaciones precisas de K y S, ya que el nivel óptimo de inversión puede extraerse analíticamente de estos parámetros. De hecho, cuando no se tiene en cuenta ningún otro efecto, la inversión que produce el máximo rendimiento sobre la inversión (ROI) puede calcularse como:

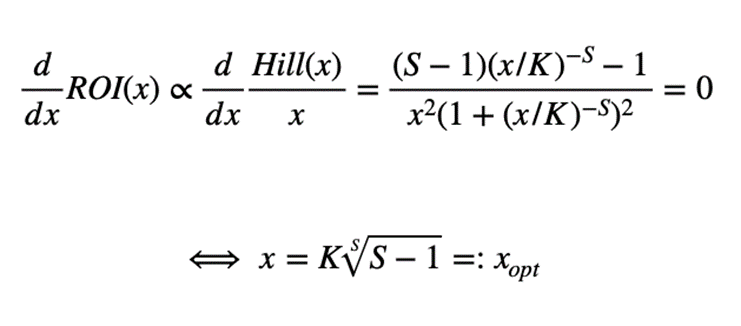
Ecuación 2. Derivación del nivel óptimo de inversión a partir de los parámetros de saturación

Obsérvese que esta inversión óptima existe para S>1 y que siempre está comprendida entre una y tres veces el valor K de semisaturación (puede comprobarse verificando los valores que puede asumir la raíz S).

El segundo efecto que debe tenerse en cuenta es la asignación temporal de los ingresos, después de que se ejecute alguna inversión específica del canal. En efecto, la inversión y los ingresos no se producen simultáneamente, y pueden pasar algunas semanas antes de que estos últimos sean significativos. Además, algunos canales de medios de comunicación están destinados a tener efectos más localizados, mientras que otros canales pueden mantener las inversiones durante periodos más largos, generando así ingresos incluso después de periodos de tiempo relativamente largos. Ambos aspectos pueden modelizarse a través de la ecuación de Adstock que figura a continuación, mediante los parámetros theta y alpha, respectivamente. El parámetro L no necesita ser específico para cada canal y sólo puede establecerse en un valor fijo que se sepa empíricamente que es suficientemente grande, como L=13 (como se sugiere en [1]). Una vez más, se invita al lector a centrarse en las figuras 2a y 2b en lugar de en la ecuación 3.

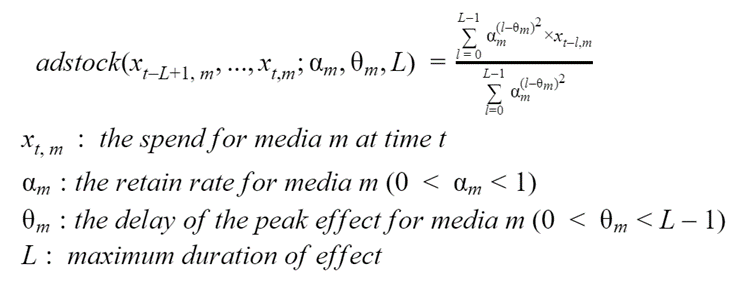
Ecuación 3. La ecuación de Adstock

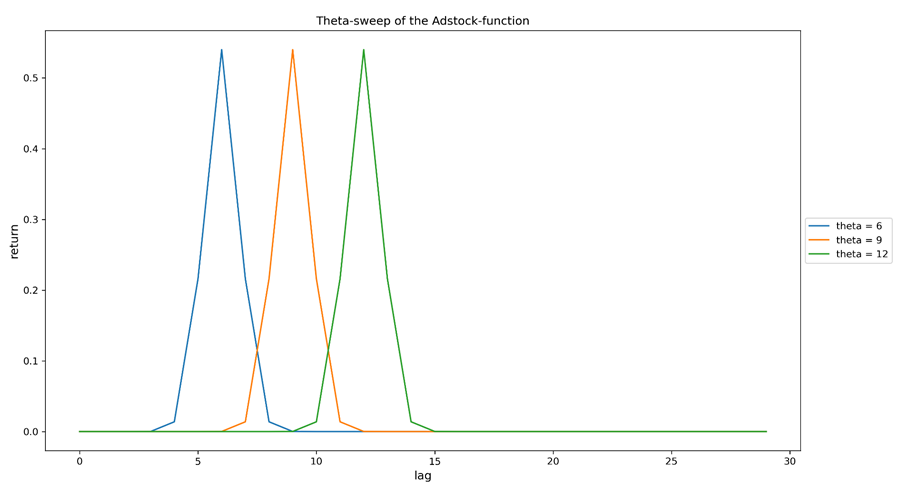
Figura 2a. Barrido del parámetro theta (retardo de pico) de la función Adstock. Todas las curvas son el resultado de una única inversión realizada en lag=0 (lag puede indicar cualquier granularidad temporal que se haya elegido en la modelización). Cuanto mayor sea theta, más tiempo tardará en observarse el ingreso máximo en relación con la inversión que lo provocó.

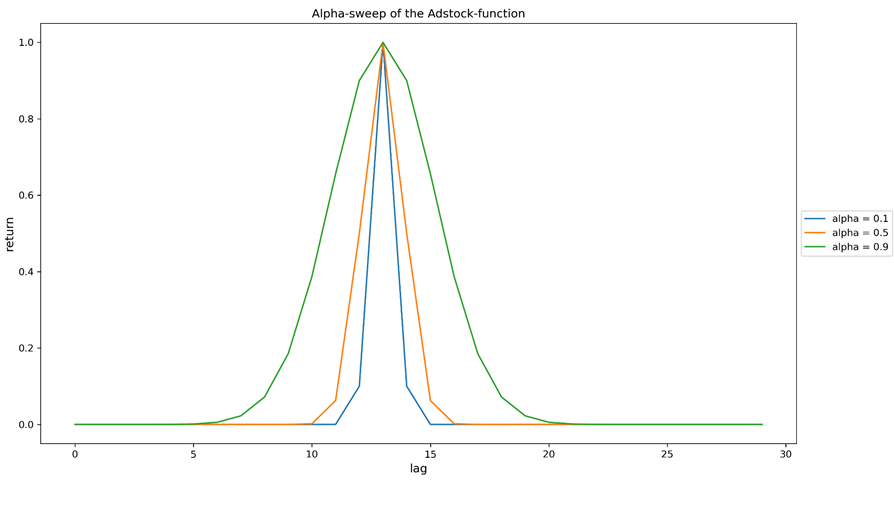
Figura 2b. Barrido del parámetro alfa (tasa de retención) de la función Adstock. Todas las curvas son el resultado de una única inversión realizada en lag=0 (lag puede indicar cualquier granularidad temporal que se haya elegido en la modelización). Cuanto mayor es alfa, más deslocalizada está la distribución de ingresos. Las curvas se han reescalado para una mejor comparación.

Una vez definidos ambos mapeos no lineales y sus respectivos parámetros, el modelo completo puede darse como sigue:

Ecuación 4. Ecuación de regresión del modelado de la combinación de medios

>Iniciemos nuestro análisis desglosando la expresión anterior. La primera observación importante es que todas las características se agrupan en inversiones en marketing y variables externas (de control), siendo la diferencia más relevante que las transformaciones de Hill y Adstock se aplican exclusivamente a las primeras. Obsérvese, por tanto, que el impacto de las características de control se considera puramente lineal e inmediato, aunque puedan añadirse efectos de tendencia y estacionalidad mediante características de desfase y estacionalidad, respectivamente. Las variables de control también pueden considerarse como el conjunto de factores ajenos al Marketing que influyen en las ventas, incluidos los precios, las ventas de la competencia, etc. Además de los términos de regresión, también tenemos en cuenta un coeficiente lineal tau y un término de ruido epsilon.

>Cuando se incluye todo, esta formulación engendra 4 parámetros no lineales para cada característica de marketing. Dependiendo del alcance del MMM y de cómo se consideren específicamente todas las acciones de marketing, nuestro modelo puede requerir varias características de marketing diferentes, lo que hace que el número de parámetros no lineales sea bastante importante. La forma de tratarlos en la modelización implica diferentes estrategias posibles, como se verá a continuación.

Los lectores más perspicaces se habrán dado cuenta de que la estadística bayesiana no se ha evocado ni una sola vez en las secciones anteriores. Esto nos lleva a preguntarnos: ¿por qué deberíamos preocuparnos por utilizar un enfoque bayesiano para ajustar este modelo, cuando se dispone de alguna observación específica data ?

Resulta que la respuesta está muy relacionada con el gran número de parámetros que hay que aproximar, un número que muy a menudo queda desbordado por la disponibilidad de data para ajustar nuestro modelo. Echemos un vistazo a la matriz Expertise x Data Availability que figura a continuación:

Figura 4.Matriz Expertise x Data Disponibilidad para el estudio Media Mix Modeling

A partir de esta matriz, debería quedar claro que la complejidad del problema a abordar aquí depende de la siguiente pregunta: ¿forma parte de nuestra tarea la aproximación de todos estos parámetros no lineales? Si no es así, es decir, si estos parámetros se conocen previamente, entonces sólo deberían aparecer como pretransformaciones en data, que luego se ajustarán a un modelo de regresión lineal multivariante simple. Este sería el caso ideal si se dispusiera de suficiente información/experiencia previa para establecer valores aproximados a estos parámetros, y estos valores simplemente no estuvieran sujetos a validación por data.

Huelga decir que el conocimiento absoluto del comportamiento de los canales entre todos los tipos de medios es una suposición bastante fuerte, y lo más probable es que como mucho se disponga de algunas pistas sobre estos parámetros para la modelización. Por lo tanto, la observación data también debe utilizarse para ajustar estos parámetros y comprender mejor los canales implicados. Si esto se combina con una baja disponibilidad de data , resulta extremadamente conveniente -o incluso necesario- utilizar toda la información conocida previamente para garantizar un buen rendimiento del modelo.

El enfoque bayesiano es, por tanto, una forma de realizar una estimación de los parámetros (de regresión y no lineales) todo en uno, que permite introducir pistas en el modelo como conocimiento previo, para obtener el mejor rendimiento con un data limitado. Veamos ahora un poco más en detalle cómo se puede conseguir esto.

El MMM bayesiano adapta un conjunto de distribuciones a priori (una para el valor de cada parámetro lineal o no lineal) en un conjunto de distribuciones a posteriori. Esto se hace mediante la exposición a data (evidencia), y las distribuciones posteriores pueden considerarse como comprensiones revisadas de cómo se comporta cada canal y contribuye a las ventas. En Python, esto puede implementarse con bibliotecas de modelado probabilístico como PySTAN o PyMC3.

Obsérvese que esta estrategia abre un nuevo conjunto de entradas controlables, aparte de la observación data: las distribuciones a priori. De hecho, hay mucha flexibilidad en la elección de la distribución para cada parámetro y en la adaptación de sus momentos en función de cada canal, lo que dará lugar a una salida diferente para la misma observación data. Mientras que en el artículo original de Google [1] reports se observó empíricamente que las distribuciones funcionaban mejor para cada tipo de parámetro(K, S, alfa, theta y beta), aquí exploraremos cómo podemos adaptarlas aún más a cada canal individual de acuerdo con los conocimientos previos sobre su comportamiento.

Antes de ahondar en las distribuciones a priori para cada parámetro, una estrategia potencialmente útil a tener en cuenta es verificar si no podemos descartar algunos de estos parámetros por completo. Esto no sólo nos ayudará a simplificar el modelo, sino también (como resultado) a obtener un mejor rendimiento en la limitada data.

De hecho, aunque en la ecuación 4 se muestra que los mapeos no lineales se aplican a todas las características de marketing, también podría ser sensato descartar una o ambas transformaciones para algunas acciones específicas: por ejemplo, si estas características se extienden a las acciones comerciales y no sólo a los canales de medios de comunicación, uno podría estar interesado en incluir las inversiones TPR (reducción temporal de precios) como una característica. Esto tiene un efecto inmediato obvio, ya que el aumento de las ventas se observa y desaparece prácticamente en el mismo momento en que se inicia y se paraliza la inversión (reducción de precios), respectivamente. Por lo tanto, puede que no interese utilizar la transformación Adstock para esta característica, que tiene la ventaja de reducir el número de parámetros que hay que estimar.

Another viable simplification can be implemented for channels whose investments are known to vary very little in time: in these cases, we are operating at only a very small section of the curves shown in Figure 1, where the relation between return and investment can be deemed approximately linear. Hence, we can discard the Hill function for these channels, as saturation will not play an important role. In more technical terms, this assumption is valid when dx<<K, where dx is some measure of historical variation on investment.

Una vez verificada la relevancia de todos los parámetros no lineales, el siguiente paso consiste en comprender cómo sus priores pueden aportar información. Hasta ahora, he utilizado a propósito el término "indicios", bastante vago desde el punto de vista técnico, para definir cualquier tipo de dato de entrada del modelo que no sea una observación estructurada en forma de tabla data. Aquí veremos algunos ejemplos de lo que podrían ser y también llenaremos el vacío entre éstas y las distribuciones a priori reales que servirán de entrada para la inferencia bayesiana, llevando este conocimiento al modelo.

Tomemos primero el ejemplo del precio en relación con la competencia. Se trata de una variable externa que intrínsecamente tiene un fuerte impacto en las ventas, por lo que podría incluirse como elemento de control en el modelo MMM. Se podría argumentar fácilmente que cuanto mayor sea este precio relativo, menores serán las ventas. Esto es de sentido común para nosotros, pero deberíamos decirle explícitamente al modelo que sólo busque soluciones con impacto negativo. Para ello, elegimos que la distribución a priori del parámetro beta asociado al precio (véase la ecuación 4) sea una media normal negativa. Hacemos lo contrario para las características con impacto positivo (por ejemplo, si se está modelando la venta de bebidas refrescantes, la temperatura media semanal debería tener un impacto positivo). Tenga en cuenta que esto no es necesario: si no está muy seguro del impacto de una característica en la variable objetivo, puede introducirle una variable a priori no informada (por ejemplo, la distribución normal estándar) y dejar que el modelo la aprenda por sí mismo.

Éste es sólo un ejemplo de cómo ajustar las distribuciones a priori para incluir conocimientos cualitativos en el modelo. Otra posible información cualitativa puede provenir, por ejemplo, de la naturaleza de una acción de marketing específica (como en el ejemplo anterior de TPR, si se decide no recortar totalmente el tiempo de retardo, sino cambiar su distribución para concentrarse sólo en los retardos muy cortos). El conocimiento previo cuantitativo, por su parte, puede proceder de estudios previos o estimaciones realizadas en el análisis histórico data . Por ejemplo, en el primer caso, la distribución de pesos de la regresión puede modificarse en función del valor del retorno de la inversión hallado en un estudio MMM anterior: el modelo puede buscar valores más pequeños o más altos desde el principio para los canales que se sabe que tienen un retorno más pequeño o más grande; en el segundo caso, la suposición de que las inversiones históricas deberían ser más o menos del mismo orden que el nivel de inversión ideal puede dar lugar a conocimientos previos informados sobre el parámetro de saturación K de la ecuación 1: de este modo, el modelo sabe qué canales son más grandes o más pequeños en términos de alcance potencial.

La matriz que figura a continuación resume algunas estrategias clave que pueden considerarse para afinar las distribuciones a priori, tanto cualitativas como cuantitativas. No se trata, ni mucho menos, de una lista exhaustiva, y la viabilidad de cada una puede variar en función del contexto y debe revisarse para cada estudio específico.

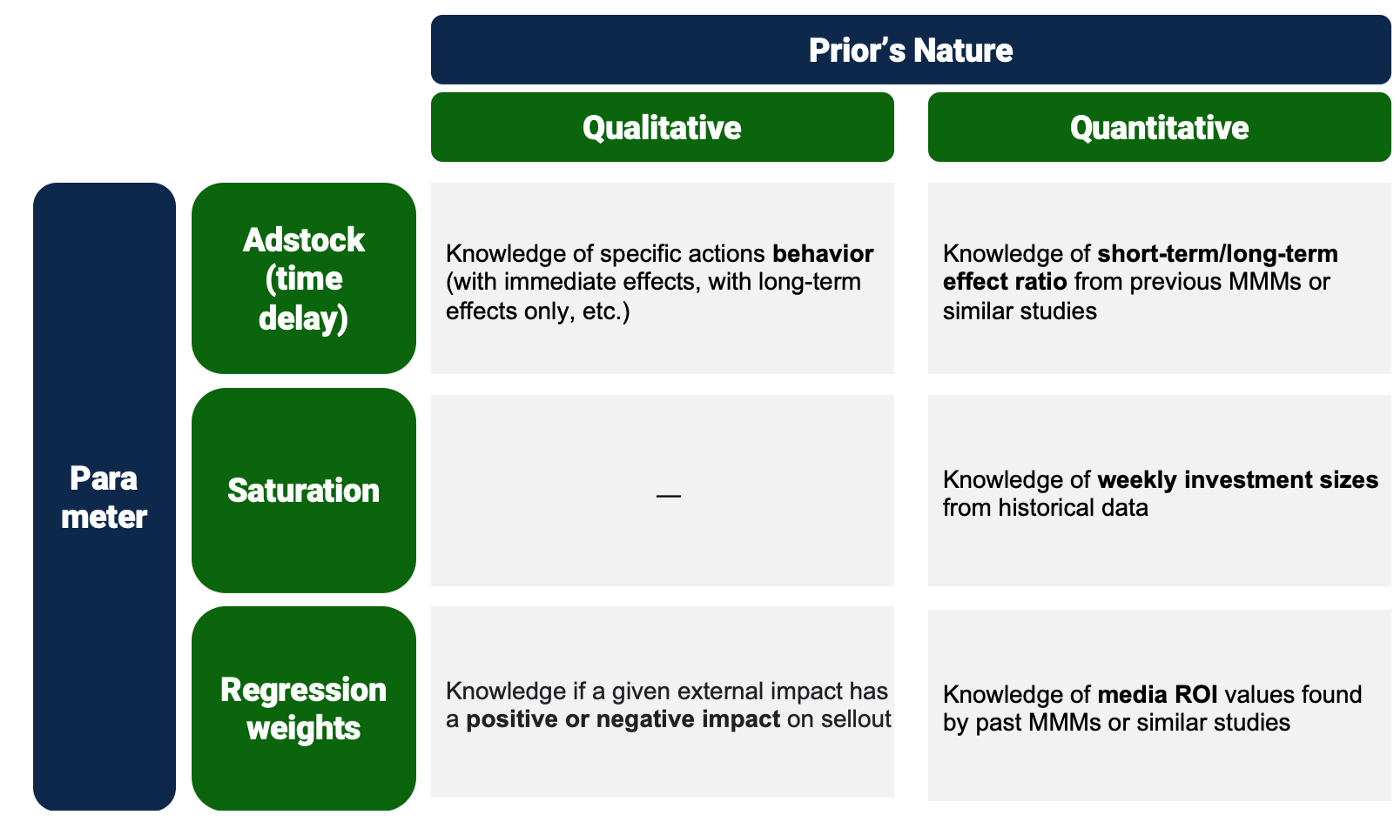
Figura 5. Ejemplo de matriz de estrategias de ajuste a priori para un caso de uso de la modelización bayesiana de la combinación de medios. Las estrategias deben variar en función del ámbito de aplicación y de los conocimientos actuales disponibles

Mientras que un estudio de Modelización de la Mezcla de Medios requiere tratar con el comportamiento de varias acciones de Marketing diferentes, el enfoque Bayesiano permite una estimación global de éstas, junto con el aumento de las ventas para cada una de estas características, así como para factores externos (características de control). Esto nos permite cosechar los datos observados disponibles en data para aprender estos comportamientos cuando no se conocen de antemano a través de la experiencia disponible o de estudios y pruebas anteriores específicos del canal. Sin embargo, esto tiene un coste, que se refleja sobre todo en la complejidad del modelo y la consiguiente necesidad de un número suficiente de data para lograr un buen rendimiento. Cuando no se satisface esta necesidad, el resultado clave es un modelo que puede fácilmente sobreajustarse a la data observada proporcionando parámetros que simplemente no son razonables.

En este artículo, hemos explorado una forma de remediar este efecto trabajando con conocimientos previos distintos de los observables data, desde las conclusiones cuantitativas de estudios anteriores hasta la comprensión empresarial cualitativa de la naturaleza de alguna característica y su impacto en las ventas. Estos conocimientos se incluyen adaptando las distribuciones a priori de cada uno de los parámetros del modelo. Aunque desde un punto de vista pragmático esto puede entenderse como un sesgo del modelo, también es una forma de evitar el ajuste excesivo del modelo a patrones que sólo se observan debido a la disponibilidad limitada de data, centrándose en combinaciones que se aproximan a lo que se conoce o al menos se espera que sea cierto. En otras palabras, adaptar las distribuciones es una forma de llegar a un compromiso entre el aprendizaje a partir de nuevas observaciones data y el respeto de los antiguos conocimientos empresariales, un compromiso que puede explorarse en varios niveles diferentes en función de lo que esté disponible en un caso específico de modelización de la combinación de medios.

Un agradecimiento especial a Camila C. Moreno, Rafael Melo, Rhayssa Sonohata, Vinicius Pacheco y Wedeueis Braz, del equipo brasileño, por revisar este artículo antes de su publicación. Artefact por revisar este artículo antes de su publicación.

[1] Jin, Y., Wang, Y., Sun, Y., Chan, D., & Koehler, J. (2017). Métodos bayesianos para el modelado de la combinación de medios con efectos de arrastre y forma.