Bayesian Media Mix Modeling with limited data

Wenn Sie schon einmal mit Problemen der Media-Mix-Modellierung (MMM) im Marketing zu tun hatten, wissen Sie vielleicht, dass diese eine ganze Reihe von kanalspezifischen Effekten (Verzögerungen, Sättigung und Langzeiteffekte) beinhalten, die jeweils durch mindestens einen anderen Parameter modelliert werden. Sie wissen vielleicht auch, dass dies nicht gerade ein Kontext ist, in dem eine Fülle von Daten und/oder Datenvariabilität zum Trainieren Ihres Modells garantiert ist. Bei klassischen MMMs sind vorherige Annahmen über das Verhalten der Medienkanäle (d. h. über die Werte für die oben genannten Parameter) erforderlich, um den Beitrag jedes Kanals zum Umsatz durch lineare Regression zu bewerten. Eine leistungsfähige Alternative dazu ist der Bayes'sche MMM-Ansatz [1], der eine umfassende Schätzung sowohl des Kanalverhaltens als auch des Umsatzanstiegs durch vorherige Verteilungen und Daten ermöglicht. Dies bedeutet, dass falsche und unveränderliche Annahmen vermieden werden, wenn in der Vergangenheit keine kanalspezifischen Studien durchgeführt wurden. Natürlich wird das Modell dadurch auch viel komplexer, und die Eingabe aller möglichen Informationen, die bei der Suche nach einer guten Lösung helfen können, wird entscheidend.

In der Tat besteht eine inhärente Gefahr darin, ein so komplexes Modell ausschließlich auf begrenzte Daten zu stützen, um zu lernen: Im Gegensatz zu den meisten Anwendungen mit Regressionsproblemen sollte ein MMM-Modell eher als beschreibendes denn als prädiktives Werkzeug dienen. Daher sind eine gute Anpassung an die Trainingsdaten und eine Verallgemeinerung auf ungesehene Daten zwar interessant, aber nicht ausreichend: Das Modell muss auch korrekte Einblicke in den tatsächlichen historischen Verkaufsanstieg, die Investitionsrendite(ROI) und die Sättigung für jeden Kanal liefern, um eine zuverlässige Ausgabe für die Planung von Marketingstrategien zu gewährleisten. Mit anderen Worten: Die Gefahr besteht darin, dass es mehrere Parameterkombinationen gibt, die die Daten korrekt abbilden, aber nicht alle davon wirklich sinnvoll sind - man könnte argumentieren, dass dies nur eine weitere Ausprägung des Fluchs der Dimensionalität ist.

Aber was bedeutet es, dass eine Lösung "wirklich sinnvoll" ist? Eine praktikable Antwort ist, dass das Modell zwar neue Muster aus den Daten lernen kann, seine Ergebnisse aber nicht völlig von dem eventuell vorhandenen Vorwissen abweichen sollten. Die Möglichkeit, diese Informationen als Vorwissen einzubeziehen (so dass wir dem Modell helfen können, eine sinnvolle Parameterkombination zu finden), ist nur einer der vielseitigen und leistungsstarken Aspekte der Bayes'schen Lösung.>

In diesem Artikel werden wir untersuchen, wie qualitatives und quantitatives Geschäftswissen in maßgeschneiderte Prioritätsverteilungen umgesetzt werden kann, die ein leistungsfähiges MMM ermöglichen, selbst wenn nur wenige Informationen aus strukturierten historischen Daten vorliegen.

Bevor wir untersuchen, wie wir Wahrscheinlichkeitsverteilungen nutzen können, um die Leistung unseres Modells zu optimieren, lassen Sie uns mit einigen Schlüsseldefinitionen für das Media Mix Modeling selbst beginnen. Im Wesentlichen basiert das MMM auf einer linearen Regression, wobei die abhängige Variable der angestrebte Umsatz ist und die unabhängigen Variablen (Merkmale) die Investitionen in verschiedene Marketingmaßnahmen sowie externe Kontrollvariablen sind, die sich ebenfalls auf den Umsatz auswirken (Preisgestaltung, Wettbewerb, Saisonalität usw.).

Es gibt jedoch einen entscheidenden Unterschied zwischen dieser Formulierung und der eines herkömmlichen linearen Regressionsmodells: Marketing-Investitionsmerkmale sollten auch eine Reihe nichtlinearer Transformationen durchlaufen, deren primäres Ziel darin besteht, erwartete Verhaltensweisen von Medienkanälen darzustellen, die nicht durch lineare Abbildungen modelliert werden können. Diese Transformationen enthalten jeweils eine Untergruppe von Parametern, die die Gesamtintensität und Art dieser Verhaltensweisen steuern. Es gibt zwei wichtige nichtlineare Zuordnungen, Sättigung und Zeitverzögerung, die im Folgenden kurz behandelt werden.

Sättigung ist ein sehr bekannter Effekt bei Marketingkanälen, der sich in einem nichtlinearen Verhältnis zwischen Investitionen und den daraus resultierenden Einnahmen niederschlägt. Dies kann als der Effekt verstanden werden, dass Anzeigen zu immer weniger relevanten Nutzern gebracht werden, oder alternativ aufgrund der relativ geringeren Zunahme der Reichweite (neue exponierte Nutzer) mit jedem zusätzlich investierten Dollar. Der Sättigungseffekt kann durch die unten dargestellte Hill-Gleichung modelliert werden. Da der genaue Ausdruck hier nicht von Interesse ist, wird der Leser gebeten, sich stattdessen auf die Abbildungen 1a und 1b zu konzentrieren, die zeigen, was mit der Hill-Funktion geschieht, wenn die Werte ihrer beiden Parameter gesweept werden.

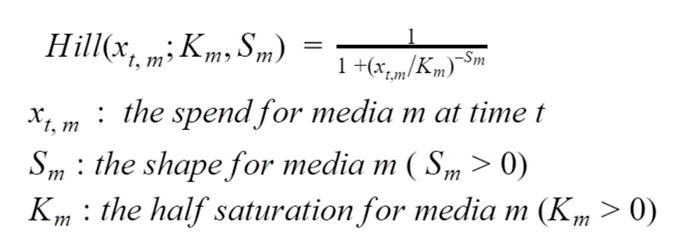
Gleichung 1. Die Hill-Gleichung

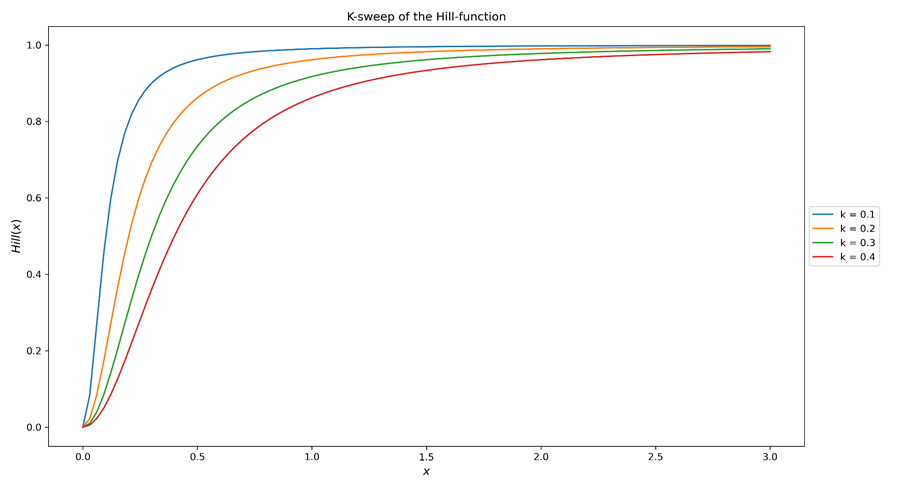
Abbildung 1a. Verschiebung des Parameters K (Halbsättigung) der Hill-Funktion. Die Gesamtform der Kurve wird in etwa beibehalten, während der Punkt der halben Sättigung (bei Hill(x)=0,5) verschoben wird. Mit anderen Worten: Je größer K ist, desto schwieriger ist es, den zugehörigen Medienkanal zu sättigen.

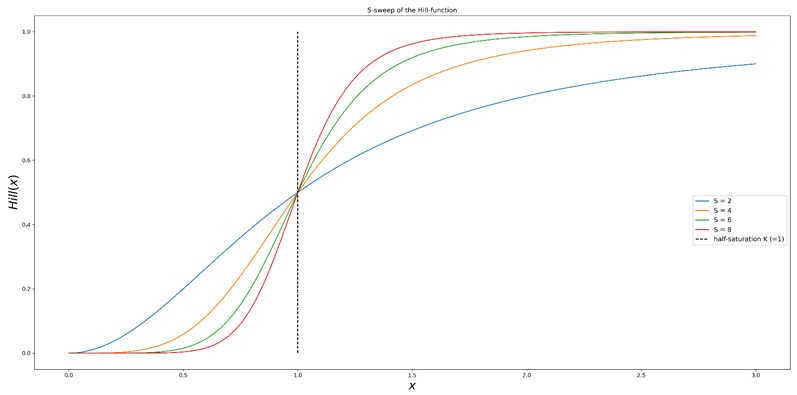
Abbildung 1b. Verschiebung des Parameters S (Form) der Hill-Funktion. Der Halbsättigungspunkt der Kurve wird beibehalten, während die Steigung um ihn herum zunimmt. Mit anderen Worten: Je größer S ist, desto größer sind die Grenzgewinne für Investitionen um den halben Sättigungspunkt herum.

Wie oben dargelegt, enthält die Hill-Gleichung zwei wichtige Parameter: Während K den Punkt der Halbsättigung definiert (der Kanal hat genau die Hälfte seiner maximalen Einnahmen, wenn die Investition gleich K ist), beeinflusst S die Form der Sättigungskurve (je höher sein Wert, desto S-förmiger wird die Kurve). Genaue Schätzungen für K und S sind von entscheidender Bedeutung, da ein optimales Investitionsniveau analytisch aus diesen Parametern abgeleitet werden kann. Wenn keine anderen Auswirkungen berücksichtigt werden, kann die Investition, die eine maximale Kapitalrendite (ROI) ergibt, wie folgt berechnet werden:

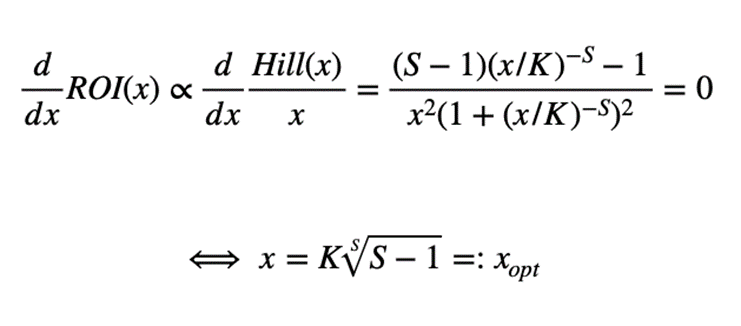
Gleichung 2. Ableitung des optimalen Investitionsniveaus aus den Sättigungsparametern

Man beachte, dass diese optimale Investition für S>1 existiert und dass sie immer zwischen dem ein- und dreifachen Wert der Halbsättigung K liegt (man kann dies überprüfen, indem man die Werte überprüft, die die S-Wurzel annehmen kann).

Der zweite Effekt, der berücksichtigt werden sollte, ist die zeitliche Verteilung der Einnahmen, nachdem einige kanalspezifische Investitionen getätigt wurden. Investitionen und Einnahmen fallen nämlich nicht gleichzeitig an, und es kann einige Wochen dauern, bis letztere spürbar werden. Darüber hinaus haben einige Medienkanäle zwangsläufig eher lokal begrenzte Auswirkungen, während andere Kanäle Investitionen über längere Zeiträume halten können und somit auch nach relativ langen Zeiträumen Einnahmen erzielen. Diese beiden Aspekte lassen sich durch die nachstehende Adstock-Gleichung mit den Parametern Theta und Alpha modellieren. Der Parameter L muss nicht für jeden Kanal spezifisch sein und kann lediglich auf einen festen Wert gesetzt werden, von dem empirisch bekannt ist, dass er hinreichend groß ist, z. B. L=13 (wie in [1] vorgeschlagen). Auch hier wird der Leser gebeten, sich auf die Abbildungen 2a und 2b statt auf Gleichung 3 zu konzentrieren.

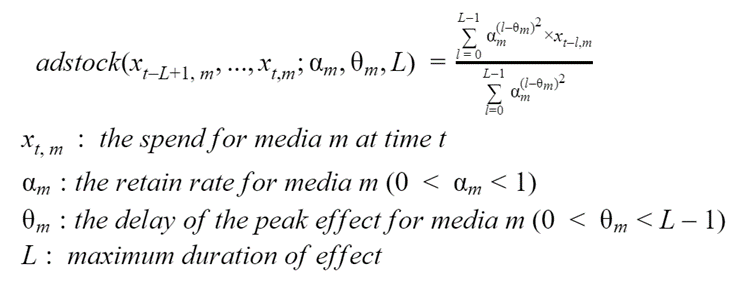
Gleichung 3. Die Adstock-Gleichung

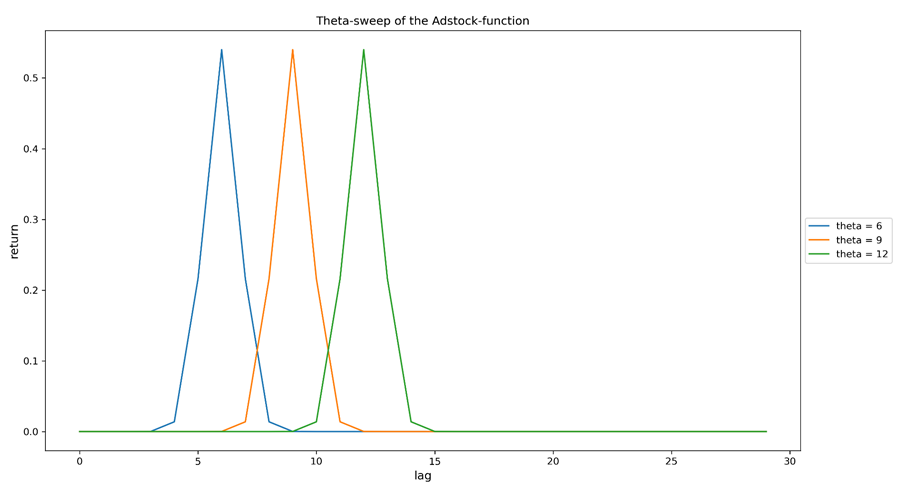
Abbildung 2a. Sweeping des Theta-Parameters (Spitzenverzögerung) der Adstock-Funktion. Alle Kurven sind das Ergebnis einer einzigen Investition, die bei lag=0 getätigt wurde (lag kann jede beliebige Zeitgranularität bezeichnen, die bei der Modellierung gewählt wurde). Je größer Theta ist, desto länger dauert es, bis der maximale Ertrag im Verhältnis zu der Investition, die ihn verursacht hat, zu beobachten ist.

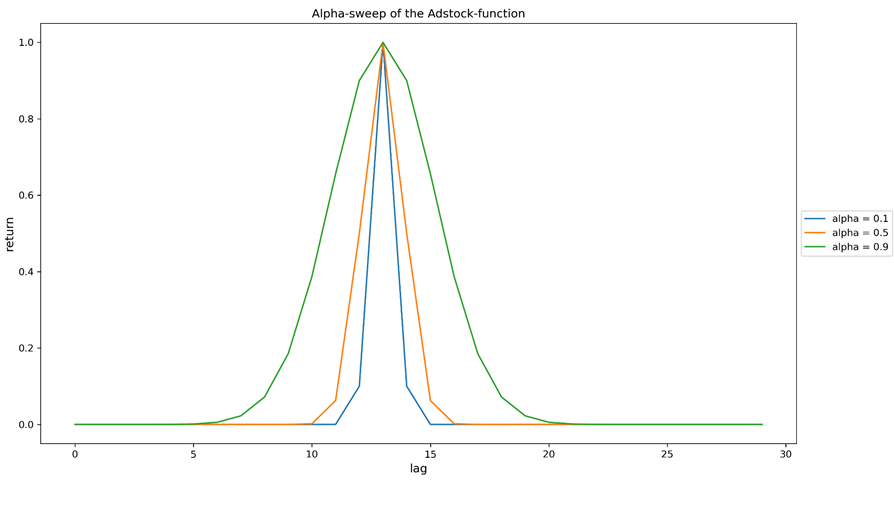
Abbildung 2b. Schwenken des Alpha-Parameters (Retentionsrate) der Adstock-Funktion. Alle Kurven sind das Ergebnis einer einzigen Investition, die zum Zeitpunkt lag=0 getätigt wurde (lag kann jede beliebige Zeitgranularität bezeichnen, die bei der Modellierung gewählt wurde). Je größer Alpha ist, desto dezentraler ist die Ertragsverteilung. Die Kurven wurden zur besseren Vergleichbarkeit neu skaliert.

Sobald die beiden nichtlinearen Abbildungen und ihre jeweiligen Parameter definiert sind, kann das vollständige Modell wie folgt angegeben werden:

Gleichung 4. Media-Mix-Modellierung Regressionsgleichung

>Beginnen wir unsere Analyse, indem wir den obigen Ausdruck aufschlüsseln. Die erste wichtige Beobachtung ist, dass alle Merkmale in Marketinginvestitionen und externe (Kontroll-)Variablen unterteilt sind, wobei der wichtigste Unterschied darin besteht, dass die Hill- und Adstock-Transformationen ausschließlich auf erstere angewendet werden. Es ist also zu beachten, dass die Auswirkungen der Kontrollvariablen als rein linear und unmittelbar angesehen werden, auch wenn Trend- und Saisoneffekte durch Lag- bzw. Saisoneffekte hinzugefügt werden können. Kontrollvariablen können auch als eine Reihe von Faktoren außerhalb des Marketings betrachtet werden, die sich auf den Absatz auswirken, einschließlich der Preisgestaltung, des Absatzes der Wettbewerber usw. Neben den Regressionstermini berücksichtigen wir auch einen linearen Koeffizienten tau und einen Rauschterm epsilon.

>Wenn alles einbezogen wird, ergeben sich aus dieser Formulierung 4 nichtlineare Parameter für jedes Marketingmerkmal. Je nach Umfang des MMM und je nachdem, wie spezifisch alle Marketingaktionen betrachtet werden, kann unser Modell mehrere verschiedene Marketingmerkmale erfordern, wodurch die Anzahl der nichtlinearen Parameter recht wichtig wird. Die Art und Weise, wie diese in der Modellierung behandelt werden, impliziert verschiedene mögliche Strategien, wie im Folgenden erörtert wird.

Dem aufmerksamen Leser wird aufgefallen sein, dass die Bayes'sche Statistik in den vorangegangenen Abschnitten nicht ein einziges Mal erwähnt wurde. Dies wirft die Frage auf: Warum sollten wir einen Bayes'schen Ansatz für die Anpassung dieses Modells verwenden, wenn einige spezifische Beobachtungsdaten zur Verfügung stehen?

Es stellt sich heraus, dass die Antwort sehr stark mit der großen Anzahl von Parametern zusammenhängt, die approximiert werden müssen - eine Anzahl, die oft nicht mit der Datenverfügbarkeit übereinstimmt, um unser Modell anzupassen. Werfen wir einen Blick auf die nachstehende Matrix aus Fachwissen und Datenverfügbarkeit:

Abbildung 4:Matrix aus Fachwissen und Datenverfügbarkeit für die Media-Mix-Modellierungsstudie

Aus dieser Matrix sollte ersichtlich sein, dass die Komplexität des hier zu lösenden Problems von der folgenden Frage abhängt: Ist die Annäherung all dieser nichtlinearen Parameter Teil unserer Aufgabe? Wenn nicht - d. h. wenn diese Parameter bereits bekannt sind -, dann sollten sie nur als Vor-Transformationen der Daten erscheinen, die dann in ein einfaches lineares multivariates Regressionsmodell eingepasst werden. Dies ist idealerweise der Fall, wenn genügend frühere Informationen/Expertise zur Verfügung stehen, um Näherungswerte für diese Parameter festzulegen, und diese Werte einfach nicht durch Daten validiert werden können.

Es erübrigt sich zu sagen, dass die absolute Kenntnis des Kanalverhaltens bei allen Medientypen eine ziemlich starke Annahme ist, und die Chancen stehen gut, dass höchstens einige Anhaltspunkte für diese Parameter für die Modellierung verfügbar sind. Daher müssen auch die Beobachtungsdaten verwendet werden, um diese Parameter anzupassen und die beteiligten Kanäle besser zu verstehen. Wenn dies mit einer geringen Datenverfügbarkeit gepaart ist, wird es äußerst praktisch - oder sogar erforderlich - alle zuvor bekannten Informationen zu verwenden, um eine gute Modellleistung zu gewährleisten.

Der Bayes'sche Ansatz ist also eine Möglichkeit, eine umfassende Schätzung von Parametern (Regression und nichtlineare Parameter) vorzunehmen, die es ermöglicht, Hinweise als Vorwissen in das Modell einzugeben, um eine optimale Leistung bei begrenzten Daten zu erzielen. Gehen wir nun etwas mehr ins Detail, wie dies erreicht werden kann.

Das Bayes'sche MMM passt eine Reihe von Vorabverteilungen (eine für den Wert jedes linearen oder nichtlinearen Parameters) an eine Reihe von Nachabverteilungen an. Dies geschieht anhand von Daten (Evidenz), und die posterioren Verteilungen können als überarbeitete Erkenntnisse darüber angesehen werden, wie sich jeder Kanal verhält und zum Umsatz beiträgt. In Python kann dies mit probabilistischen Modellierungsbibliotheken wie PySTAN oder PyMC3 umgesetzt werden.

Beachten Sie, dass diese Strategie neben den Beobachtungsdaten eine neue Gruppe von kontrollierbaren Inputs eröffnet: die Prioritätsverteilungen. In der Tat gibt es viel Flexibilität bei der Wahl der Verteilung für jeden Parameter und bei der Anpassung ihrer Momente an jeden Kanal, was dann zu einer anderen Ausgabe für dieselben Beobachtungsdaten führt. Während der ursprüngliche Google-Artikel [1] über Verteilungen berichtet, bei denen empirisch beobachtet wurde, dass sie für jeden Parametertyp(K, S, Alpha, Theta und Beta) besser abschneiden, werden wir hier untersuchen, wie wir diese auf jeden einzelnen Kanal entsprechend dem bisherigen Wissen über ihr Verhalten weiter zuschneiden können.

Bevor wir uns mit den Vorverteilungen für die einzelnen Parameter befassen, sollten wir prüfen, ob wir nicht einige dieser Parameter ganz weglassen können. Dies wird uns nicht nur helfen, das Modell zu vereinfachen, sondern auch (als Folge davon) eine bessere Leistung bei begrenzten Daten zu erzielen.

Obwohl die nichtlinearen Zuordnungen auf alle Marketingmerkmale in Gleichung 4 angewandt werden, könnte es auch sinnvoll sein, eine oder beide Transformationen für einige spezifische Aktionen zu verwerfen: Wenn diese Merkmale beispielsweise auf Handelsaktionen und nicht nur auf Medienkanäle ausgedehnt werden, könnte man daran interessiert sein, TPR-Investitionen (vorübergehende Preissenkungen) als Merkmal aufzunehmen. Dies hat eine offensichtliche unmittelbare Auswirkung, da der Umsatzanstieg praktisch im selben Moment beobachtet und beendet wird, in dem die Investition (Preissenkung) beginnt bzw. ergriffen wird. Daher könnte es uninteressant sein, die Adstock-Transformation für dieses Merkmal zu verwenden, die den Vorteil hat, dass sie die Anzahl der zu schätzenden Parameter reduziert.

Another viable simplification can be implemented for channels whose investments are known to vary very little in time: in these cases, we are operating at only a very small section of the curves shown in Figure 1, where the relation between return and investment can be deemed approximately linear. Hence, we can discard the Hill function for these channels, as saturation will not play an important role. In more technical terms, this assumption is valid when dx<<K, where dx is some measure of historical variation on investment.

Sobald die Relevanz aller nichtlinearen Parameter nachgewiesen ist, besteht der nächste Schritt darin, zu verstehen, wie ihre Prioritäten Informationen enthalten können. Bisher habe ich absichtlich den technisch eher vagen Begriff "Hinweise" verwendet, um jede Art von Modelleingabe zu definieren, die keine strukturierten, tabellenartigen Beobachtungsdaten sind. Hier werden wir uns einige Beispiele dafür ansehen, was dies sein könnte, und auch die Lücke zwischen diesen und den tatsächlichen Prioritätsverteilungen füllen, die als Input für die Bayes'sche Inferenz dienen und dieses Wissen in das Modell tragen.

Nehmen wir zunächst das Beispiel des Preises im Verhältnis zur Konkurrenz. Hierbei handelt es sich um eine externe Variable, die sich naturgemäß stark auf den Absatz auswirkt und daher als Kontrollmerkmal in das MMM-Modell aufgenommen werden könnte. Man könnte ganz einfach argumentieren, dass der Umsatz umso geringer ist, je höher der relative Preis ist. Das ist für uns einleuchtend, aber wir sollten dem Modell ausdrücklich sagen, dass es nur nach Lösungen mit negativen Auswirkungen suchen soll. Dies erreichen wir, indem wir die Prioritätsverteilung für den mit dem Preis verbundenen Parameter Beta (siehe Gleichung 4) als negative Halbnormalverteilung wählen. Bei Merkmalen mit positiver Auswirkung verhält es sich umgekehrt (z. B. sollte die wöchentliche Durchschnittstemperatur eine positive Auswirkung haben, wenn Sie den Verkauf von Erfrischungsgetränken modellieren). Beachten Sie, dass dies keine Notwendigkeit ist: Wenn Sie sich über die Auswirkung eines Merkmals auf die Zielvariable nicht ganz sicher sind, können Sie es mit einem uninformierten Prior (z. B. der Standardnormalverteilung) füttern und das Modell es selbst lernen lassen.

Dies ist nur ein Beispiel dafür, wie man Prioritätsverteilungen abstimmen kann, um qualitatives Wissen in das Modell einzubeziehen. Andere mögliche qualitative Informationen können z. B. aus der Art einer bestimmten Marketingaktion stammen (wie in dem zuvor genannten Beispiel für TPR, wenn man beschließt, die Zeitverzögerung nicht ganz zu kürzen, sondern ihre Verteilung so zu verschieben, dass sie sich nur auf sehr kurze Verzögerungen konzentriert). Quantitatives Vorwissen hingegen kann aus früheren Studien oder Schätzungen stammen, die auf der Analyse historischer Daten beruhen. Als Beispiel für Ersteres kann die Regressionsgewichtsverteilung entsprechend dem ROI-Wert verschoben werden, der in einer früheren MMM-Studie ermittelt wurde - das Modell kann dann von Anfang an nach kleineren/höheren Werten für Kanäle suchen, von denen bekannt ist, dass sie kleinere/größere Renditen haben; was Letzteres betrifft, kann die Annahme, dass historische Investitionen in etwa in der gleichen Größenordnung wie das ideale Investitionsniveau liegen sollten, zu informierten Prioritäten für den Sättigungsparameter K aus Gleichung 1 führen - das Modell ist somit darüber informiert, welche Kanäle in Bezug auf die potenzielle Reichweite größer oder kleiner sind.

Die nachstehende Matrix fasst einige Schlüsselstrategien zusammen, die für die Abstimmung von qualitativen und quantitativen Prioritätsverteilungen in Betracht gezogen werden können. Diese Liste ist keineswegs erschöpfend, und die Durchführbarkeit der einzelnen Strategien kann je nach Kontext variieren und sollte für jede spezifische Studie überprüft werden.

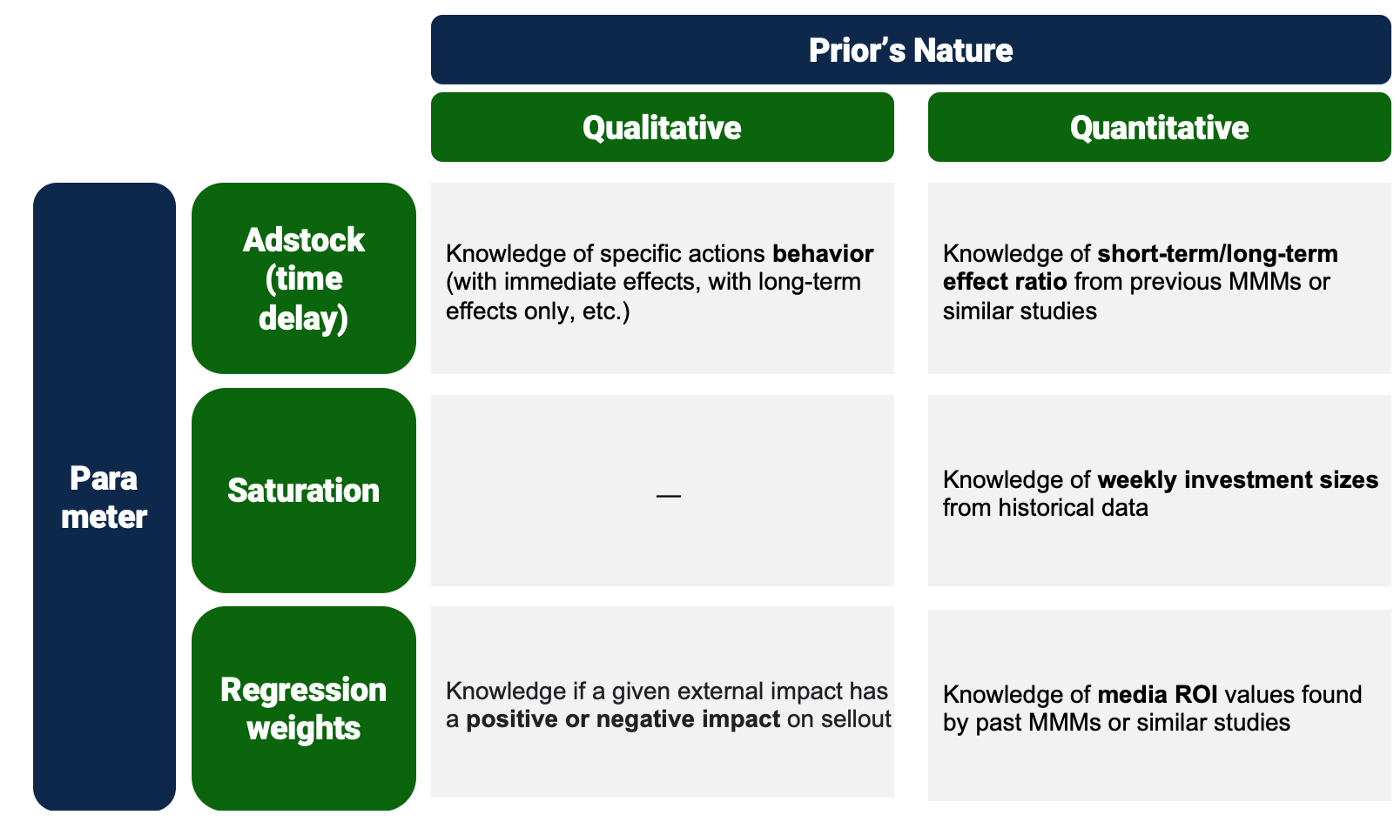
Abbildung 5. Beispiel für eine Prior-Tuning-Strategie-Matrix für einen Anwendungsfall der Bayes'schen Medienmix-Modellierung. Die Strategien sollten je nach Umfang und verfügbarem aktuellen Wissen variieren

Während bei einer Media-Mix-Modellierungsstudie das Verhalten mehrerer verschiedener Marketingmaßnahmen untersucht werden muss, ermöglicht der Bayes'sche Ansatz eine umfassende Schätzung dieser Maßnahmen, zusammen mit der Umsatzsteigerung für jedes dieser Merkmale sowie für externe Faktoren (Kontrollmerkmale). Auf diese Weise können wir die verfügbaren Beobachtungsdaten nutzen, um diese Verhaltensweisen zu erlernen, wenn sie nicht schon vorher durch vorhandenes Fachwissen oder frühere kanalspezifische Studien und Tests bekannt sind. Dies ist jedoch mit Kosten verbunden, die sich vor allem in der Komplexität des Modells und dem daraus resultierenden Bedarf an ausreichenden Daten zur Erzielung einer guten Leistung niederschlagen. Wenn dieser Bedarf nicht gedeckt ist, kann ein Modell die beobachteten Daten leicht übererfüllen, indem es Parameter ausgibt, die einfach nicht angemessen sind.

In diesem Artikel haben wir eine Möglichkeit erforscht, diesen Effekt zu beheben, indem wir mit anderen Vorkenntnissen als den beobachtbaren Daten arbeiten, von quantitativen Schlussfolgerungen aus früheren Studien bis hin zu qualitativen geschäftlichen Erkenntnissen über die Art einiger Merkmale und deren Auswirkungen auf den Umsatz. Diese werden berücksichtigt, indem die Vorverteilungen der einzelnen Modellparameter angepasst werden. Während dies aus pragmatischer Sicht als Verzerrung des Modells verstanden werden kann, ist es auch eine Möglichkeit, eine Überanpassung des Modells an Muster zu vermeiden, die nur aufgrund der begrenzten Verfügbarkeit der Daten beobachtet werden, indem man sich auf Kombinationen konzentriert, die nahe an dem liegen, was bekannt ist oder zumindest als wahr erwartet wird. Mit anderen Worten: Die Anpassung von Verteilungen ist ein Kompromiss zwischen dem Lernen aus neuen Beobachtungsdaten und dem Respektieren von altem Geschäftswissen - ein Kompromiss, der auf verschiedenen Ebenen erforscht werden kann, je nachdem, was in einem bestimmten Media-Mix-Modellierungsfall verfügbar ist.

Besonderen Dank an Camila C. Moreno, Rafael Melo, Rhayssa Sonohata, Vinicius Pacheco und Wedeueis Braz vom brasilianischen Artefact Team für die Durchsicht dieses Artikels vor der Veröffentlichung.

[1] Jin, Y., Wang, Y., Sun, Y., Chan, D., & Koehler, J. (2017). Bayes'sche Methoden für die Modellierung des Medienmixes mit Carryover- und Shape-Effekten.